Question

A circle is inscribed in an equilateral triangle of side a. The area of any square inscribed in a circle is:
A) $ \dfrac{{{a^2}}}{4} $
B) $ \dfrac{{{a^2}}}{6} $
C) $ \dfrac{{{a^2}}}{9} $
D) $ \dfrac{{2{a^2}}}{3} $

Answer 1

Hint: Draw the diagram according to the question: A circle inside a triangle and a square inside this circle. Then by applying geometry, the side of the square can be found and then its area can be calculated.
Important things to remember:
Area of a square = $ {\left( {side} \right)^2} $
All sides of an equilateral triangle are equal and angles are of measure 60 degrees
 $ \tan \theta = \dfrac{P}{B} $
 $ \sin \theta = \dfrac{P}{H} $ where,
P = Perpendicular
B = Base
H = Hypotenuse

Complete step-by-step answer:
A circle inscribed in a triangle of side ‘a’ and a square inscribed inside that circle is given as:

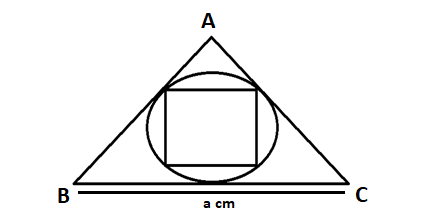
Now, to calculate the area of this square, say PQRS, we need to draw the medians of the triangle.

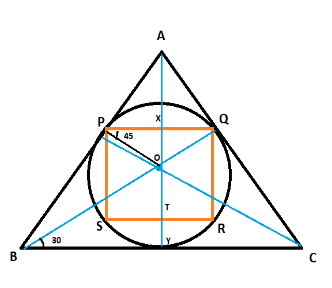
In $ \vartriangle OBY $ :
 $ \angle OBY $ = 30°
(Since $ \angle ABY $ = 60°; angle of an equilateral triangle.
 $ \angle OBY $ = $ \dfrac{1}{2}\angle ABY $ ; median bisects the angle, so
 $ \angle OBY $ = $ \dfrac{1}{2} \times 60 $ = 30° )
BY = $ \dfrac{a}{2} $ (since the median divides BC into half)
Calculating the value of $ \tan \theta $ for this triangle:
 $ \tan \theta = \dfrac{P}{B} $ here,
Perpendicular (P) = OY
Base (B) = BY
Substituting:
 $
  \tan \theta = \dfrac{{OY}}{{BY}} \\
  \tan {30^o} = \dfrac{{OY}}{{\dfrac{a}{2}}}\left( {\because \theta = \angle OBC = {{30}^o}} \right) \\
  \dfrac{1}{{\sqrt 3 }} = \dfrac{{OY}}{{\dfrac{a}{2}}} \\
\Rightarrow OY = \dfrac{a}{{2\sqrt 3 }} \\
  $
Now, OX = OY; radius of the circle:
The side of the square is PQ
 $ \angle POQ $ = 45° (As the complete is 90°)
Calculating the value of $ \sin \theta $ for $ \vartriangle POQ $ :
 $ \sin \theta = \dfrac{P}{H} $ here,
Perpendicular (P) = PX
Hypotenuse (H) = OX = OY
Substituting:
\[
\Rightarrow \sin \theta = \dfrac{{PX}}{{OY}} \\
\Rightarrow \sin {45^o} = \dfrac{{PX}}{{OY}}\left( {\because \theta = \angle POQ = 45} \right) \\
  PX = OY\sin {45^o} \\
 \]
Side of square = PQ
PQ = 2 PX (bisected by median)
 $ \Rightarrow $ PQ = 2 OY sin 45°
Substituting the value of OY, we get:
 $
\Rightarrow PQ = 2OY\sin {45^o} \\
\Rightarrow PQ = 2 \times \dfrac{a}{{2\sqrt 3 \times \sqrt 2 }} \\
\Rightarrow PQ = \dfrac{a}{{\sqrt 6 }} \\
  $
This side of the square is $ \dfrac{a}{{\sqrt 6 }} $
Area of the square is given by squaring the side:
$\Rightarrow$ Area = $ {\left( {PQ} \right)^2} $
$\Rightarrow$ Area = $ {\left( {\dfrac{a}{{\sqrt 6 }}} \right)^2} $
$\Rightarrow$ Area = $ \dfrac{{{a^2}}}{6} $
Therefore, the required area of the inscribed square is $ \dfrac{{{a^2}}}{6} $ , thus option (B) is correct
So, the correct answer is “Option B”.

Note: All the median from vertices bisect the angles as well as the edge at which they form an intercept (touch).
The point O where medians from all the vertices meet is called its centroid.
Be careful while performing geometrical calculations
For an angle remember, the edge opposite to it will be its perpendicular.