Question

A circle cutting the circle \[{{x}^{2}}+{{y}^{2}}=4\]orthogonally and having its center on the line \[2x-2y+9=0\] passes through two fixed points. Those points are
\[\begin{align}
  & 1.(4,0)\text{ and (0,4)} \\
 & \text{2}\text{.}(-4,4)\text{ and }\left( \dfrac{-1}{2}\text{,}\dfrac{1}{2} \right) \\
 & \text{3}\text{.}(-4,0)\text{ and (4,0)} \\
 & \text{4}\text{.}(4,-4)\text{ and }\left( \dfrac{1}{2}\text{,}\dfrac{-1}{2} \right) \\
\end{align}\]

Answer 1

Hint: Suppose, the circle to be \[{{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0\]. As per the orthogonal circle condition, get the relationship between the coordinate of the assumed circle (f, g) put (f, g) in the line passing through the center of the assumed circle. Thus, find C. The final equation would consist of a circle and a line, solving them desired points would come.

Complete step by step answer:
The question talks about the intersection of two circles orthogonally or we can say perpendicularly. Generalized equation of a circle is:
\[{{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0\]
Where, coordinates of center are = (-g, -f) and $\sqrt{c}$ = radius of circle.
When two circles with equations:
\[\begin{align}
  & {{x}^{2}}+{{y}^{2}}+2{{g}_{1}}x+2{{f}_{1}}y+{{c}_{1}}=0 \\
 & {{x}^{2}}+{{y}^{2}}+2{{g}_{2}}x+2{{f}_{2}}y+{{c}_{2}}=0 \\
\end{align}\]
Intersect each other orthogonally, then
\[2{{g}_{1}}{{g}_{2}}+2{{f}_{1}}{{f}_{2}}={{c}_{1}}+{{c}_{2}}\]
Here, we have the equation of 1 circle given as:
\[\begin{align}
  & {{x}^{2}}+{{y}^{2}}=4\Rightarrow {{x}^{2}}+{{y}^{2}}-4=0 \\
 & {{g}_{1}}=0,{{f}_{1}}=0,{{c}_{1}}=-4;\text{ Center = }\left( 0,0 \right) \\
\end{align}\]
Suppose, the second circle cutting this circle orthogonally is:
\[{{x}^{2}}+{{y}^{2}}+2{{g}_{2}}x+2{{f}_{2}}y+{{c}_{2}}=0\]
Center of second circle is (-g, -f)
Given that, the center of the second circle lies on the line $2x-2y+9=0$. So, the coordinates (-g, -f) must also lie on this line and satisfy the line equation.

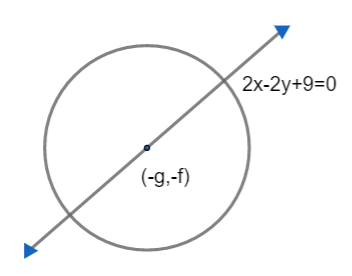
\[\begin{align}
  & 2x-2y+9=0 \\
 & 2\left( -g \right)-2\left( -f \right)+9=0 \\
 & 2g=2f+9\text{ }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. (i)} \\
\end{align}\]
Name this equation as 1.
Circle 1 and circle 2 are cutting each other perpendicularly, therefore:
\[\begin{align}
  & 2{{g}_{1}}{{g}_{2}}+2{{f}_{1}}{{f}_{2}}={{c}_{1}}+{{c}_{2}} \\
 & \left( 2\times 0\times {{g}_{2}} \right)+\left( 2\times 0\times {{f}_{2}} \right)=-4+{{c}_{2}} \\
 & \Rightarrow {{c}_{2}}=-4 \\
\end{align}\]
Now, re-writing the equation of circle 2 using the ${{c}_{2}}$ value and equation (1)
\[\begin{align}
  & {{x}^{2}}+{{y}^{2}}+\left( 2f+9 \right)x+2fy+4=0 \\
 & \Rightarrow \left( {{x}^{2}}+{{y}^{2}}+9x+4 \right)+f\left( 2x+2y \right)=0 \\
\end{align}\]
This can be viewed as:
The circle ${{x}^{2}}+{{y}^{2}}+9x+4=0$ is being cut by the line $2x+2y=0$
Now, \[2x+2y=0\]
\[\Rightarrow y=-x\]
Solving two above equations:

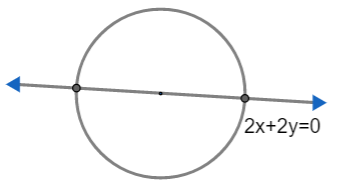
\[\begin{align}
  & {{x}^{2}}+{{\left( -x \right)}^{2}}+9x+4=0 \\
 & \Rightarrow 2{{x}^{2}}+9x+4=0 \\
 & \Rightarrow 2{{x}^{2}}+8x+x+4=0 \\
 & \Rightarrow 2x\left( x+4 \right)+\left( x+4 \right)=0 \\
 & \Rightarrow \left( x+4 \right)\left( 2x+1 \right)=0 \\
 & \Rightarrow x=-4\text{ and x=}\dfrac{-1}{2} \\
\end{align}\]
Putting value of $x=-4\text{ in }2x+2y=0$ line equation, we get $y=-\left( -4 \right)=4$
Therefore, (x, y) = (-4, 4)
Similarly at \[x=\dfrac{-1}{2},y=\dfrac{1}{2};\left( \dfrac{-1}{2},\dfrac{1}{2} \right)\]
Thus, required coordinate are \[\left( -4,4 \right)\left( \dfrac{-1}{2},\dfrac{1}{2} \right)\]

So, the correct answer is “Option 2”.

Note: The line passing through the circle must not be confused with the line intersecting the circle at two points of the second circle. Usually students make mistake in writing the orthogonality condition as \[\text{2}{{\text{g}}_{\text{1}}}{{\text{g}}_{\text{2}}}+\text{2}{{\text{f}}_{\text{1}}}{{\text{f}}_{\text{2}}}+{{\text{c}}_{\text{1}}}{{\text{c}}_{\text{2}}}=0\]. Here constant terms are added on the RHS and not multiplied and added with terms on the LHS. To recollect this, they can recollect that condition for perpendicular lines is slopes, \[{{\text{m}}_{\text{1}}}\times {{\text{m}}_{\text{2}}}=-\text{1}\]. So, here we can write the coefficients of variables x and y in equation of circle as \[\text{2}{{\text{g}}_{\text{1}}}{{\text{g}}_{\text{2}}}+\text{2}{{\text{f}}_{\text{1}}}{{\text{f}}_{\text{2}}}\] and then equate them to constants, i.e. \[{{\text{c}}_{\text{1}}}{{\text{c}}_{\text{2}}}\]