Question

A circle cuts two perpendicular lines so that each intercept is of given length. The locus of the centre of the circle is a conic whose eccentricity is
A) 1
B) $\dfrac{1}{\sqrt{2}}$
C) $\sqrt{2}$
D) None of these.

Answer 1

Hint: Let the two perpendicular lines be the x-axis and the y-axis, and let the intercepts be equal to a and b, respectively. Assume the centre of the circle to be (x,y). Use the property that the perpendicular from the centre of the circle divides the chord into two equal halves.
Complete step-by-step answer:
Let us start the solution by letting the two perpendicular lines be the x-axis and the y-axis, and the intercepts be equal to a and b, respectively. We will also assume the centre of the circle to be (x,y).
Let us draw the diagram of the situation according to the assumed data.

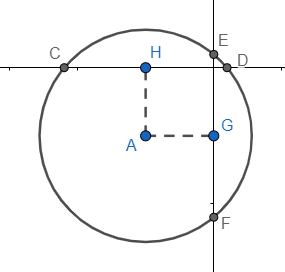
Now, as we have considered A to be (x,y) , the point H comes out to be (x,0) and G comes to be (0,y).
Also, according to our assumption, CD=a and EF=b and they are the chords of the circle.
Now we know that the perpendicular from the centre of the circle divides the chord into two equal halves. So, we can say that HD = $\dfrac{1}{2}CD=\dfrac{a}{2}$ and GE = $\dfrac{1}{2}EF=\dfrac{b}{2}$
Now, according to the distance formula, the distance between two points $\left( {{x}_{1}},{{y}_{1}} \right)\text{ and }\left( {{x}_{2}},{{y}_{2}} \right)$ is given by $\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$ .
So, using the figure and above result, we can say that $E=\left( 0,y+\dfrac{b}{2} \right)$ and $D=\left( x+\dfrac{a}{2},0 \right)$ . Also, we can see that E and D lie on the circle and the A is the centre, so AE=AD=radius.
$\Rightarrow \sqrt{{{\left( x-0 \right)}^{2}}+{{\left( y-\left( y+\dfrac{b}{2} \right) \right)}^{2}}}=\sqrt{{{\left( x-\left( x+\dfrac{a}{2} \right) \right)}^{2}}+{{\left( y-0 \right)}^{2}}}$
$\Rightarrow \sqrt{{{x}^{2}}+\dfrac{{{b}^{2}}}{4}}=\sqrt{\dfrac{{{a}^{2}}}{4}+{{y}^{2}}}$
If we square both sides of the equation, we get
${{x}^{2}}+\dfrac{{{b}^{2}}}{4}=\dfrac{{{a}^{2}}}{4}+{{y}^{2}}$
$\Rightarrow {{x}^{2}}-{{y}^{2}}=\dfrac{{{a}^{2}}}{4}-\dfrac{{{b}^{2}}}{4}$
\[\Rightarrow \dfrac{{{x}^{2}}}{\dfrac{{{a}^{2}}}{4}-\dfrac{{{b}^{2}}}{4}}-\dfrac{{{y}^{2}}}{\dfrac{{{a}^{2}}}{4}-\dfrac{{{b}^{2}}}{4}}=1\]
So, looking at the equation, we can say that the locus of the centre is a hyperbola with the length of major axis=length of the minor axis. We know that the eccentricity of a hyperbola is given by:
$e=\sqrt{1+\dfrac{{{\left( \text{length of minor axis} \right)}^{2}}}{{{\left( \text{length of major axis} \right)}^{2}}}}=\sqrt{1+\left( \dfrac{\dfrac{{{a}^{2}}}{4}-\dfrac{{{b}^{2}}}{4}}{\dfrac{{{a}^{2}}}{4}-\dfrac{{{b}^{2}}}{4}} \right)}=\sqrt{1+1}=\sqrt{2}$
Therefore, the answer to the above question is option (c).

Note: You could have also solved the question by taking any two perpendicular lines, but considering the axes as the lines is the smartest way of approaching the above problem. Also, be sure that you learn all the properties and theorems related to circles as they are used very often.