Question

A church tower stands on the bank of a river, which is $150feet$ wide, and on the top of the tower is a spire $30feet$ high. To an observer on the opposite bank of the river, the spire subtends the same angle that a pole six feet high subtends when placed upright on the ground at the foot of the tower. Prove that the height of the tower is nearly $285feet$ .

Answer 1

Hint:To solve this question we should about the trigonometric identity:
Trigonometry: It deals with the relationship of side of a triangle with the angles.
As, $\sin \theta = \dfrac{{perpendicular}}{{hypotenuse}}$
 $\cos \theta = \dfrac{{base}}{{hypotenuse}}$
 $\tan \theta = \dfrac{{perpendicular}}{{base}}$

Complete step by step answer:
In this question we draw diagrams according to given data.

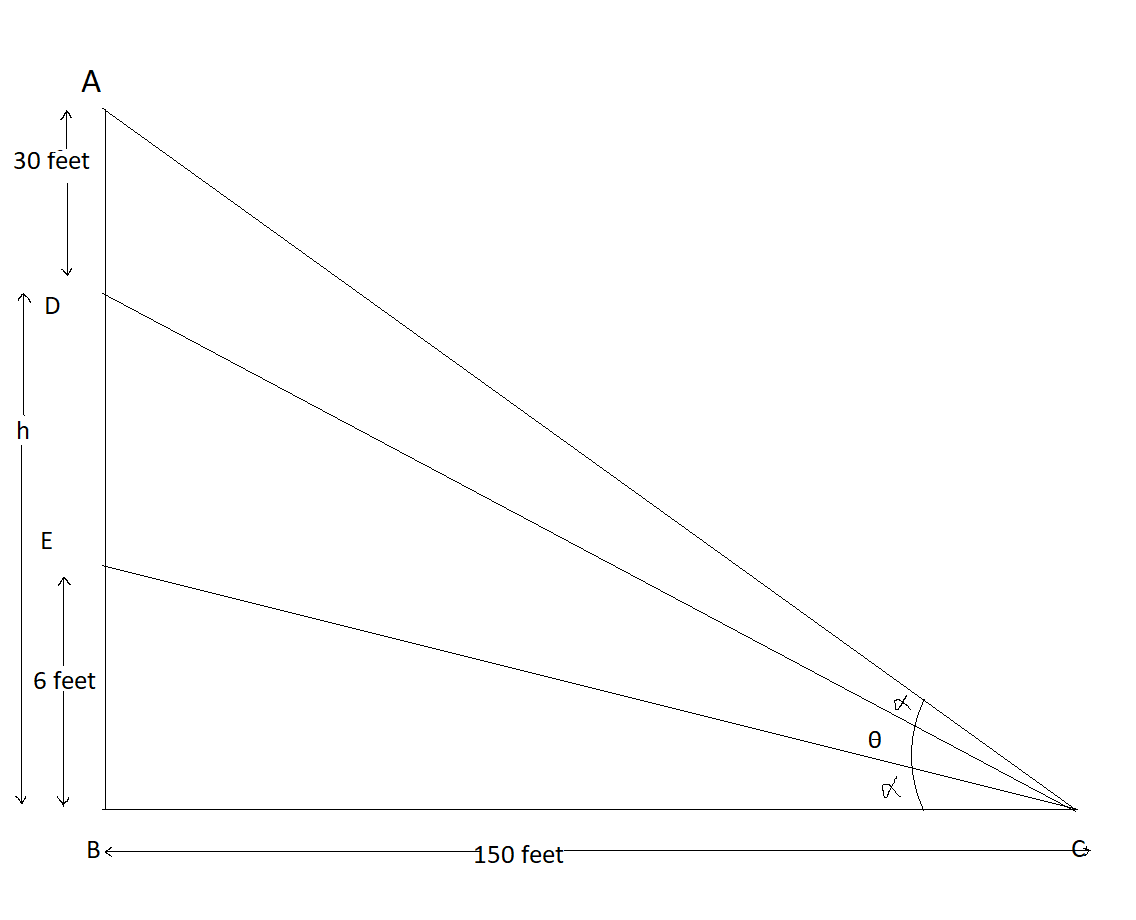
As we had drawn the figure as per given data.
We will see observer is at C. and BD is height of the church.
So, as given in the question
 $\angle ADC = \angle EBC$
As we look at $\Delta ECB$ we get,
Let $\angle EBC = \alpha $
 $\tan \alpha = \dfrac{6}{{150}} = \dfrac{1}{{25}}$ …….. $(1)$
(By using $\tan \theta = \dfrac{{prendicular}}{{base}}$ )
Let $\angle DCE = \theta $ and $BD = h$ , height of the church,
In $\Delta DCB$ ,
 $\tan DCB = \dfrac{h}{{150}}$
  $\tan (\alpha + \theta ) = \dfrac{h}{{150}}$ ……. $(2)$
In $\Delta ABC$ . We get,
 $\angle ABC = \theta + 2\alpha $
And
 $\tan ABC = \dfrac{{AB}}{{BC}} = \dfrac{{h + 30}}{{150}}$
 $\tan (\theta + 2\alpha ) = \dfrac{{h + 30}}{{150}}$ ……. $(3)$
Now we can write,
 $\tan (\theta + 2\alpha ) = \tan ((\theta + \alpha ) + \alpha )$
By using, $\tan (\theta + \alpha ) = \dfrac{{\tan \theta + \tan \alpha }}{{1 - \tan \theta \tan \alpha }}$ . We get,
 $\tan (\left( {\theta + \alpha } \right) + \alpha ) = \dfrac{{\tan \left( {\theta + \alpha } \right) + \tan \alpha }}{{1 - \tan \left( {\theta + \alpha } \right)\tan \alpha }}$
From $(3)$ , $(2)$ and $(1)$ . we get,
 $ \Rightarrow \dfrac{{h + 30}}{{150}} = \dfrac{{\dfrac{h}{{150}} + \dfrac{6}{{150}}}}{{1 - \dfrac{h}{{150}} \times \dfrac{6}{{150}}}}$
 By further solving it,
 $ \Rightarrow \dfrac{{h + 30}}{{150}} = \dfrac{{150(h + 6)}}{{{{150}^2} - 6h}}$
 $ \Rightarrow \left( {h + 30} \right)\left( {{{150}^2} - 6h} \right) = {150^2}(h + 6)$
  \[ \Rightarrow {150^2}h - 6{h^2} + 675000 - 180h = {150^2}h + 135000\]
 \[ \Rightarrow - 6{h^2} + 675000 - 180h = 135000\]
 \[ \Rightarrow - 6{h^2} + 675000 - 180h - 135000 = 0\]
By simplifying it we get,
 \[ \Rightarrow {h^2} + 30h - 90000 = 0\]
We now have a quadratic equation.
Solve this quadratic equation. We get,
 ${h_1} = - 315.37,{h_2} = 285.374$
As we know height cannot we a negative value.
Hence, $h = 285.374 \approx 285feet$
Hence proved the height of the church is $285feet$ .


Note: Trigonometry is used in our daily life. Main application of trigonometry is in construction work. It is also used to calculate the unknown height just by using a visible instrument which is used to measure angle created by the top of the height to the surface.