Question

A chord PQ of a circle of radius 10cm subtends an angle of \[{60^ \circ }\]at the center of the circle. Find the area of the major and minor segments of the circle.

Answer 1

Hint: A chord of a circle is the straight line drawn between the ends point of the circle where the diameter is the longest chord passing through the center joining both endpoints at the circumference. Segments are referred to as the region bounded by the chord of a circle. Whenever a cord is drawn for a circle it divides the circle into two parts and in the case of short chords circle are divide into two parts which are not equal in the region, the part having held greater region is the major segment of the circle where else part with lesser region is minor segments.

Complete step-by-step answer:
Radius \[r = 10cm\], Angle subtended \[\theta = {60^ \circ }\]

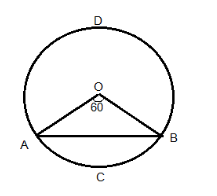
Let us find the area of the sector subtended by the sector OACB by using the formula \[\dfrac{\theta }{{360}}\pi {r^2}\]
\[
  \dfrac{\theta }{{360}}\pi {r^2} = \dfrac{{60}}{{360}} \times \pi \times {10^2} \\
   = \dfrac{1}{6} \times 3.14 \times 100 \\
   = 52.33c{m^2} \\
 \]
Now let us find the area of \[\vartriangle OAB\]which is the major segment of the sector, where
\[OA = OB = r = 10cm\]
\[\angle OAB = \angle OBA\] (\[OA = OB\])
We know the total internal angle of a triangle is equal to \[{180^ \circ }\], hence
\[
  \angle OAB + \angle OBA + \angle AOB = {180^ \circ } \\
  \angle OAB + \angle OBA = {180^ \circ } - {60^ \circ } \\
  2\left( {\angle OAB} \right) = {120^ \circ } \\
  \angle OAB = {60^ \circ } \\
 \]
Hence, we can say that \[\vartriangle OAB\]is an equilateral triangle, since
\[\angle OAB = \angle OBA = \angle AOB = {60^ \circ }\]
Hence, the area of the equilateral triangle with its side’s length $r$ is \[{A_e} = \dfrac{{\sqrt 3 }}{4}{r^2}\]
\[
  \dfrac{{\sqrt 3 }}{4}{r^2} = \dfrac{{\sqrt 3 }}{4} \times 10 \times 10 \\
   = 43.30c{m^2} \\
 \]
Now find the minor segment ABC which is equal to
Area of minor segment ABC = Area of sector OACB – Area of \[\vartriangle OAB\]
\[
  ABC = 52.33 - 43.30 \\
   = 9.03c{m^2} \\
 \]
Hence the area of major sector ADB will be equal to
Area of major segment= Area of the circle – Area of minor segment
\[
  ADB = \left( {\pi {r^2}} \right) - 9.03 \\
   = \left( {3.14 \times 10 \times 10} \right) - 9.03 \\
   = 314 - 9.03 \\
   = 304.97c{m^2} \\
 \]
Note: When a segment of a circle is divided by a chord then, the region which occupies the majority of the area is known as a major segment and that which occupies a minority of the area is known as a minor segment.