Question

A chord of a parabola cuts the axis of the parabola at O. The feet of the perpendiculars from P and P’ on the axis are M and M’ respectively. If V is the vertex then VM, VO, VM’ are
(a) A.P
(b) G.P
(c) H.P
(d) AP, GP

Answer 1

Hint: To solve this question we will first take an equation of a parabola and then try to draw its figure using the given points in the question. Any point P on the parabola is of the form \[P\left( a{{t}^{2}},2at \right)\] where t varies. We will use that the slope of the line with endpoints is given by \[\dfrac{{{y}_{1}}-{{y}_{2}}}{{{x}_{1}}-{{x}_{2}}}\] where \[\left( {{x}_{1}},{{y}_{1}} \right)\] and \[\left( {{x}_{2}},{{y}_{2}} \right)\] are the endpoints.

Complete step-by-step answer:
To solve this question, we will first consider some parabola. To do that let us define a parabola and some examples. The parabola is the locus of points in that plane that are equidistant from both the directrix and the focus. Another description of a parabola is a conic section, created from the intersection of a right circular conical surface and a plane parallel to another plane that is tangential to the conical surface. The examples of the standard parabola are:
\[\left( I \right){{y}^{2}}=x\]
It is drawn as

\[\left( II \right)y={{x}^{2}}\]
It is drawn as

  From these, let the parabola be \[{{y}^{2}}=4ax\]

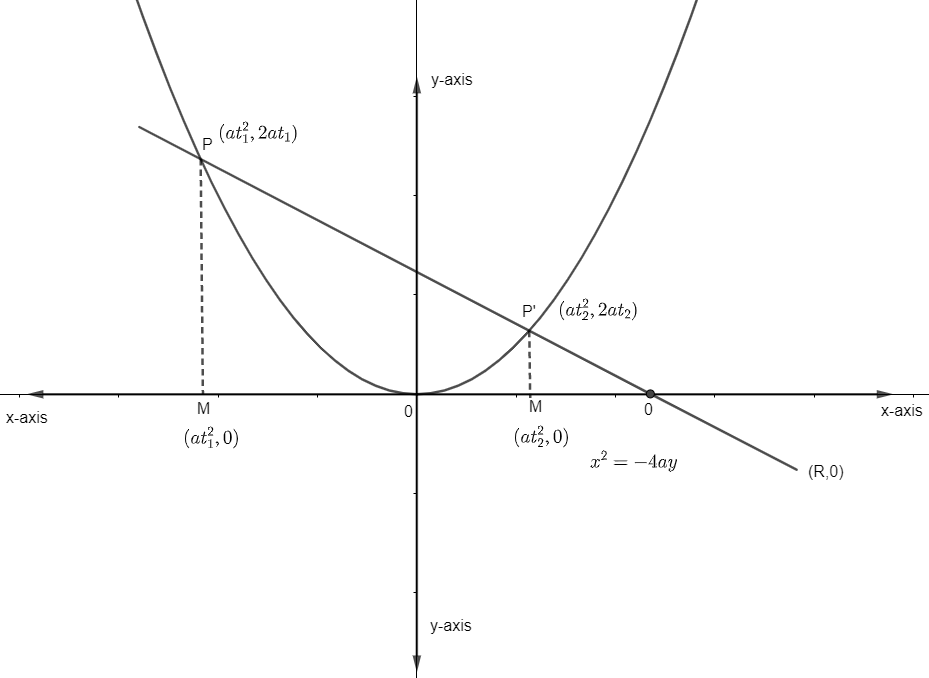
Let the vertex of parabola be V = (0, 0). The chord PP’ cuts x-axis at 0 and let it be (R, 0).
\[\Rightarrow VO=R\]
Let \[P=\left( a{{t}_{1}}^{2},2a{{t}_{1}} \right)\] be the coordinates of the point P. This is so as any point on the parabola is of the form \[P=\left( a{{t}^{2}},2at \right)\] where t varies. Then the foot of the perpendicular on the axis is \[M=\left( a{{t}_{1}}^{2},0 \right)\] (as visible by the diagram) and similarly for \[{{P}^{'}}=\left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)\] the foot of the perpendicular is \[{{M}^{'}}\left( a{{t}_{2}}^{2},0 \right)\] the coordinate of the point (0, 0). The slope of the line having endpoints as \[\left( {{x}_{1}},{{y}_{1}} \right)\] and \[\left( {{x}_{2}},{{y}_{2}} \right)\] is given by \[\dfrac{{{y}_{1}}-{{y}_{2}}}{{{x}_{1}}-{{x}_{2}}}.\] Then for PO, the slope is given by the slope of \[PO=\dfrac{2a{{t}_{1}}}{a{{t}_{1}}^{2}-R}.\]
Similarly, the slope of P’O is given by (using the above formula) the slope of \[{{P}^{'}}O=\dfrac{-2a{{t}_{2}}}{R-a{{t}_{2}}^{2}}.\]
Now because PO and P’O are forming the same line, so then the slopes are equal.
The slope of PO = Slope of P’O
\[\Rightarrow \dfrac{2a{{t}_{1}}}{a{{t}_{1}}^{2}-R}=\dfrac{-2a{{t}_{2}}}{R-a{{t}_{2}}^{2}}\]
On cross multiplying, we get,
\[\Rightarrow 2a{{t}_{1}}\left( R-a{{t}_{2}}^{2} \right)=-2a{{t}_{2}}\left( a{{t}_{1}}^{2}-R \right)\]
\[\Rightarrow {{t}_{1}}R-a{{t}_{2}}^{2}{{t}_{1}}=-a{{t}_{1}}^{2}{{t}_{2}}+{{t}_{2}}R\]
\[\Rightarrow R\left( {{t}_{1}}-{{t}_{2}} \right)=a{{t}_{2}}^{2}{{t}_{1}}-a{{t}_{1}}^{2}{{t}_{2}}\]
\[\Rightarrow R=\dfrac{a{{t}_{1}}{{t}_{2}}\left( {{t}_{2}}-{{t}_{1}} \right)}{\left( {{t}_{1}}-{{t}_{2}} \right)}\]
\[\Rightarrow R=-a{{t}_{1}}{{t}_{2}}\]
Hence, the value of R is \[-a{{t}_{1}}{{t}_{2}}.\]
So, we have,
\[VO=R\]
\[VM=a{{t}_{1}}^{2}\]
\[V{{M}^{'}}=a{{t}_{2}}^{2}\]
\[\Rightarrow V{{O}^{2}}={{R}^{2}}\]
Substituting \[R=-a{{t}_{1}}{{t}_{2}}\]
\[\Rightarrow V{{O}^{2}}={{R}^{2}}\]
\[\Rightarrow V{{O}^{2}}={{\left( -a{{t}_{1}}{{t}_{2}} \right)}^{2}}\]
\[\Rightarrow V{{O}^{2}}={{a}^{2}}{{t}_{1}}^{2}{{t}_{2}}^{2}\]
\[\Rightarrow V{{O}^{2}}=a{{t}_{1}}^{2}a{{t}_{2}}^{2}\]
\[\Rightarrow V{{O}^{2}}=VM.V{{M}^{'}}\]
\[\Rightarrow {{\left( VO \right)}^{2}}=VM.V{{M}^{'}}\]
Hence, VM, VO, VM’ are in GP.

So, the correct answer is “Option (c)”.

Note: When three numbers a, b and c are in GP, then they can be written as \[ac={{b}^{2}}.\] Here, we have obtained the answer as \[{{\left( VO \right)}^{2}}=VM.V{{M}^{'}}\] the number using the above stated theory are in GP.