Question

A child swinging on a swing in sitting position, when she stands up then the time period of the swing will
A) Increase
B) Decrease
C) Remain the same
D) Increase of the child is long and decrease if the child is short

Answer 1

Hint:Child swings are the same as a simple pendulum; hence we know in a simple pendulum the time period is directly proportional to the length of the string.
In sinusoidal wave motion, the particle moves about the mean equilibrium or the mean position with passage of time. The particle rises till they reach the highest point and the fall to its lowest point, and this cycle repeats in a uniform pattern. So the total time taken by the particle to complete this cycle is known as time period.
The time period is formulated as \[T = \dfrac{{2\pi }}{\omega }\]

Complete step by step answer:
Given the child initially is sitting on the swing and this swing behaves same as a simple pendulum where the swing reaches to a maximum height ‘A’ and then comes back to the minimum point ‘O’

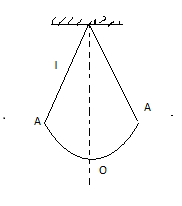
Hence the time period will be equal to\[T = \sqrt {\dfrac{l}{g}} \], where l is the effective length
Therefore we can see \[T \propto \sqrt l \]

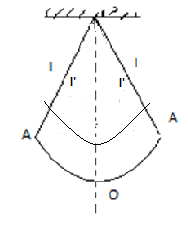
Now it is said that child stands up hence the effective length of the swing decreases and as we know time period is proportional to the length of the swing \[T \propto \sqrt l \], hence when the length of the swing decrease then time period will also decrease
\[T \propto \sqrt {l'} \]
Option (B) is correct.

Note:Students must note that the time period of the simple pendulum does not depend on the mass of the object, but it depends on the length of the string.