Question

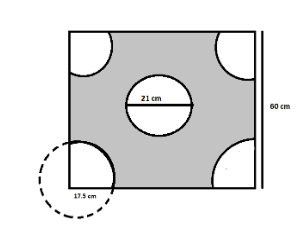
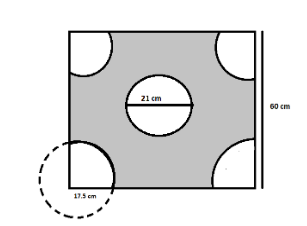
A child prepares a poster on ‘Save Energy’ on a square sheet whose each side measures 60 cm. At each corner of the sheet, she draws a quadrant of radius17.5 cm in which she shows the ways to save energy. At the centre, she draws a circle of diameter 21 cm and writes a slogan in it. Find the area of the remaining sheet.

Answer 1

Hint: The area occupied by different shapes on the sheet can be subtracted from the total area of the sheet to find the remaining or unoccupied area of the sheet.
Area of a square = $ {\left( s \right)^2} $ where s is the length of the side.
Area of a circle = $ \pi {r^2} $ where r is the radius of the circle
Quadrant of a circle has one- fourth area of the circle 🡪 $ \dfrac{{\pi {r^2}}}{4} $

Complete step-by-step answer:

Given:
Each side of sheet (s) = 60 cm
Radius of corner quadrants = 17.5 cm
Diameter of inner circle (d) = 21 cm
Now, the areas for different figures present in the sheet are given as:
Area of sheet = Area of square
(As sheet is in the shape of a square – given)
 $ \Rightarrow $ Area of sheet = $ {\left( s \right)^2} $
 $ \Rightarrow $ Area of sheet = $ {\left( {60cm} \right)^2} $ [As side of sheet is 60 cm]
 $ \Rightarrow $ Area of sheet = 3600 $ c{m^2} $ ___________ (1)
 $ \Rightarrow $ The area of inner circle = $ \pi {r^2} $
radius (r) of inner circle = $ \dfrac{d}{2} $ [since radius is half the diameter]
 $ r = \dfrac{{21}}{2} $
r = 10.5 cm, substituting:
 $ \Rightarrow $ The area of inner circle = $ \pi {\left( {10.5} \right)^2} $
                                           = $ \dfrac{{22}}{7} \times 10.5 \times 10.5 $
The area of inner circle = 346.5 $ c{m^2} $ ____________ (2)

Quadrant is one - fourth part of a circle, so its area is also one-fourth of the circle:
 $ \Rightarrow \dfrac{{\pi {r^2}}}{4} $
There are 4 quadrants present on the sheet with radius 17.5 cm, there area is:
 $ \Rightarrow 4 \times \dfrac{{\pi {r^2}}}{4} = 4 \times \dfrac{{\pi {{(17.5)}^2}}}{4} $
 $ \Rightarrow $ The area of 4 quadrants = $ \dfrac{{22}}{7} \times 17.5 \times 17.5 $
 $ \Rightarrow $ The area of 4 quadrants = 962.5 $ c{m^2} $ _________ (3)
Now,
The area of sheet left is given by difference the total area of sheet and the combined occupied area of inner circle and 4 quadrants.
 $ \Rightarrow $ Required area = equation (1) – [equation (2) + equation (3)]
 $ \Rightarrow $ Required area = 3600 – [962.5 + 346.5]
                           = 3600 – 1309
 $ \Rightarrow $ Required area = 2291 $ c{m^2} $
Therefore, the area of the remaining sheet of the given poster is 2291 $ c{m^2} $ .

Note: Always complete the answer with respective units. The area is always in square units.
  $ {m^2}/c{m^2} $
The circle in different parts can be divided as quadrants:
As four quadrants make 1 circle, its area is one- fourth of the circle.