Question

A chess board contains 32 black and 32 white squares. How many squares are along each side of the game board?

Answer 1

Hint: Assume that there are ‘n’ squares along each side of the chess game board. Consider ‘x’ as the length of each small square. Now, use the area relation that ‘area of these 64 small squares will be equal to the square of n times the length of each small square along each side’. Cancel the common factors and find the value of ‘n’.

Complete step-by-step solution:
Here, we have been provided with the information that a chessboard has 32 black and 32 white squares. We are asked to determine the number of squares along each side of the chess board.
Let us assume that there are ‘n’ small squares along each side of the chessboard and the length of each side of these small squares is ‘x’. So, we have,

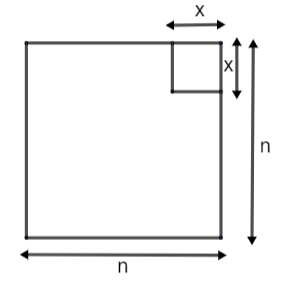
\[\because \] Total number of squares = Number of (black squares + white squares)
\[\Rightarrow \] Total number of squares = 32 + 32 = 64
So, there are 64 small squares in a chess board, therefore the area of these 64 small squares must be equal to \[nx\times nx\], because each side contains n small squares and the length of each side of these squares is x. So, we have on equating the areas,
\[\begin{align}
  & \Rightarrow nx\times nx=64\times {{x}^{2}} \\
 & \Rightarrow {{n}^{2}}{{x}^{2}}=64{{x}^{2}} \\
\end{align}\]
Cancelling the common factor from both the sides, we get,
\[\Rightarrow {{n}^{2}}=64\]
Taking square root on both the sides, we have,
\[\begin{align}
  & \Rightarrow n=\sqrt{64} \\
 & \Rightarrow n=8 \\
\end{align}\]
Hence, there are 8 small squares along each side of the chess board.

Note: One may check the answer by considering 8 columns and 8 rows in the game board and adding eight times. Remember that there are alternate black and white squares in the game board. In the above question there was no need of assuming the length of each side of the small square as x, we can directly get the answer by taking under root of the number 64 because in the end the variable x is getting cancelled.