Question

A charge q is uniformly distributed over the surface of a non-conducting disc of the radius r.The disc rotates about an axis perpendicular to its plane and passes through its centre with an angular velocity. As a result of this rotation a magnetic field of induction b is obtained at the centre of the disc if we keep both the amount of charge placed on the disk and its angular velocity to be constant and vary the radius of the disc then the variation of the magnetic induction at the centre of the disc will be represented by the figure :
A)

B)

C)

D)

Answer 1

Hint: Given, the amount of charge placed on the disk and angular velocity is kept constant. We must figure out the relation between the magnetic field of induction at the centre of disc and the radius of the disc using the known terms.
Formulas used:
$\begin{align}
  & A=2\pi rdr \\
 & T=\dfrac{2\pi }{\omega },I=\dfrac{dQ}{T} \\
\end{align}$

Complete answer:
The radius of the disc is given as R. The total charge of the disc be Q.
Let us first find the charge per unit of area of the disc.
$\begin{align}
  & q=\dfrac{Q}{\pi {{R}^{2}}} \\
 & \\
\end{align}$
The face area of the disc will be,
$A=\pi {{R}^{2}}$
If we consider an elementary ring of disc of radius r and thickness dr, face area will then be equal to,
${{A}^{1}}=2\pi rdr$
Charge on that elementary disc will be,
$\begin{align}
  & dq=\dfrac{Q}{\pi {{R}^{2}}}\times 2\pi rdr \\
 & \Rightarrow dq=\dfrac{2Qrdr}{{{R}^{2}}} \\
\end{align}$
Also, the time of rotation of disc,
$T=\dfrac{2\pi }{\omega }$
Current I associated with rotating ring is,
$\begin{align}
  & I=\dfrac{dq}{T} \\
 & \Rightarrow I=\dfrac{Q\omega dr}{\pi {{R}^{2}}} \\
\end{align}$
Therefore, the total magnetic field of induction will be,
$\eqalign{
  & B = \int\limits_0^R {\dfrac{{{\mu _0}Q\omega dr}}{{2\pi {R^2}}}} \cr
  & \Rightarrow B = \dfrac{{{\mu _0}Q\omega }}{{2\pi R}} \cr
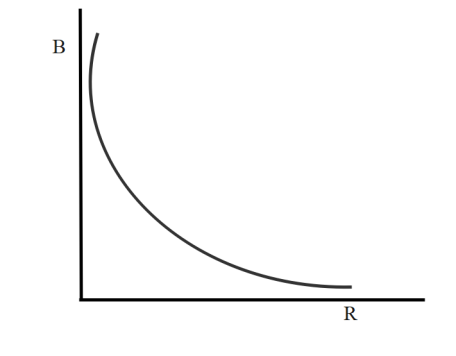
  & \Rightarrow B \propto \dfrac{1}{R} \cr} $
In the above, as charge and angular velocity are constant, variation must be a rectangular hyperbola.

Therefore, the correct option that displays rectangular hyperbola is option (A).

Additional information:
Electromagnetic induction or magnetic induction is the production of an electro motive force cross and conductor in a changing magnetic field. Michael Faraday is the one who discovered the electromagnetic induction in conductors. He mathematically described it as Faraday's laws of induction. Lenz law describes the direction of the induced field. Faraday's law was later generalized to become the Maxwell Faraday equation, one of the 4 Maxwell equations in his theory of electromagnetism. Electromagnetic induction has found many applications, including electrical components such as inductors and transformers, and devices such as electric motors and generators.

Note:
A magnetic field is a quantity that has both magnitude and direction. The magnetic field lines always emerge from the north pole and merge in the south pole. Most of us think the magnetic field only has magnitude, but it's false because it also gives us direction.