Question

A charge Q is uniformly distributed over a long rod AB of length L as shown in the figure. The electric potential at the point O lying at distance L from the end A is

A. $\dfrac{Q}{{8\pi {\varepsilon _0}L}}$
B. $\dfrac{{3Q}}{{4\pi {\varepsilon _0}L}}$
C. $\dfrac{Q}{{4\pi {\varepsilon _0}L\ln 2}}$
D. $\dfrac{{Q\ln 2}}{{4\pi {\varepsilon _0}L}}$

Answer 1

Hint: Due to a charge there will be an electric field at a point. If we integrate the electric with distance then we will get potential. Due to continuous distribution of charge the potential at a particular point can be found by integration.
Formula used:
$dV = \dfrac{{kdq}}{x}$

Complete answer:

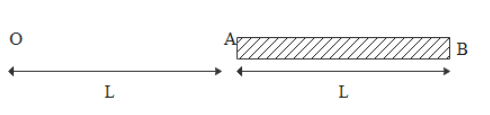
If we clearly see the diagram given we were asked to find potential due to the rod at point O.
The distance between the O and starting point of rod i.e A is L and the length of the rod is L.
Since the charge distribution on the rod is uniform and it is distributed all over the length of the rod, first we will find out the potential due to small element ‘dx’ on the point O and then integrate all over the length of the rod to find out the overall potential.
Let charge distributed per unit length be $\lambda $
So we have for small rod element ‘dx’ charge is ‘dq’
$\lambda = \dfrac{{dq}}{{dx}}$
$ \Rightarrow dq = \lambda dx$
Potential due t that small charge element is
$dV = \dfrac{{kdq}}{x}$
$k = \dfrac{1}{{4\pi {\varepsilon _0}}},\lambda = \dfrac{Q}{L}$
Substitute $dq = \lambda dx$ in $dV = \dfrac{{kdq}}{x}$ and integrate it over rod limits i.e L to 2L, then we will get
$dV = \dfrac{{kdq}}{x}$
$\eqalign{
  & \Rightarrow dV = \dfrac{{k\lambda dx}}{x} \cr
  & \Rightarrow V = \int\limits_L^{2L} {\dfrac{{k\lambda dx}}{x}} \cr
  & \Rightarrow V = \dfrac{Q}{{4\pi {\varepsilon _0}L}}\int\limits_L^{2L} {\dfrac{{dx}}{x}} \cr
  & \Rightarrow V = \dfrac{Q}{{4\pi {\varepsilon _0}L}}\ln 2 \cr} $

Hence option D will be the answer.

Additional information:
We can follow the same integral method to find out the electric field. By applying appropriate formulas and integrating we get an electric field as $\dfrac{Q}{{8\pi {\varepsilon _0}L}}$ which is given as option A to trick us.

Note:
The linear charge density is given as uniform. In some problems we will be given the linear charge density which is a function of the distance. Then we have to include that function also in the integration as it is not constant we should not take it out of the integral.