Question

A charge of $ + 10$C enters a uniform magnetic field parallel to its direction. What will happen to the charge?

Answer 1

Hint:Let us first get some idea about magnetic fields. A magnetic field, which is a vector field, describes the magnetic influence on moving electric charges, electric currents, and magnetic materials. In a magnetic field, a moving charge experiences a force that is perpendicular to both its own velocity and the magnetic field.

Complete step-by-step solution:
A charged particle's magnetic force is orthogonal to the magnetic field, resulting in:
$F = qvB\sin \theta $

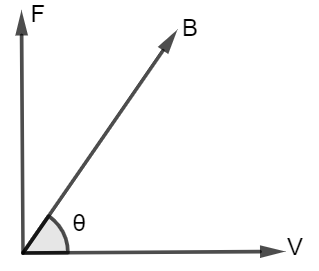
There is no net force and the charged particle goes in a straight line if its velocity is parallel to the magnetic field.
The angle between the velocity vector and the magnetic field vector B determines the force a charged particle “feels” as a result of a magnetic field. Remember that the magnetic force is equal to:
$F = qvB\sin \theta $

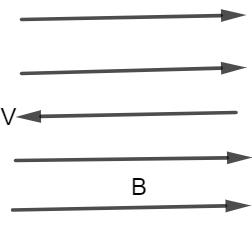
 When the magnetic field and velocity are parallel (or antiparallel), \[sin\theta = {\text{ }}0\], and no force exists. In this scenario, even in the presence of a strong magnetic field, a charged particle can continue to move in a straight line. The component of v parallel to B remains unaltered if it is between \[0\] and \[90\] degrees.

Note:In the case of a positive charge, the force exerted by an electric field is parallel to the electric field vector, while in the case of a negative charge, it is antiparallel. It is independent of the particle's velocity.