Question

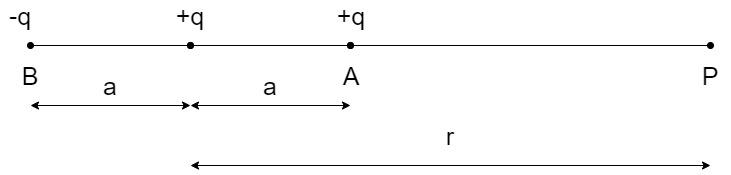
A charge configuration is shown in figure. What is the potential at a point P at a distance r on the axis, as shown assuming that $r > > a$?

Answer 1

Hint: The electric potential is defined as the work done in moving a unit positive charge from infinity to that point in the electric field, at a particular distance from the main central charge. The main basis for solving this problem is the concept that the electric potential is a scalar quantity, since it is derived from work and charge, which are scalar quantities.

Complete step by step solution:
Whenever a positive charge is in the vicinity of another positive charge, there is a repulsive force acting on the charge as explained by Coulomb's law.
The force acting on the charge per unit charge is defined by a quantity known as the electric field.
The electric field of a charge represents the influence that the charge possesses wherein it exerts an force on any charge in its vicinity which is inversely proportional to the square of distance of separation between the charges.
Thus, work has to be performed on a unit positive charge against the electric force to bring it to a point in the electric field. This work per unit charge is known as the electric potential.
If r is a point in the electric field of a charge ${q_0}$, to which a unit positive charge is to be brought from infinity, the electric potential at that point is given by –
$V = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{q_0}}}{r}$
Given that the electric potential is the work done per unit charge, we see that the electric potential is made of scalar quantities and therefore, the electric potential is a scalar quantity.
Now, given that the electric potential is a scalar quantity, the electric potential is an algebraic sum of the electric potentials due to the charges at A, B and O.
Electric potential at point P,
${V_P} = {V_A} + {V_B} + {V_O}$
This can be written as –
${V_P} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{q_A}}}{{r - a}} + \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{q_B}}}{{r + a}} + \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{q_O}}}{r}$
where ${q_O}$, ${q_A}$ and ${q_B}$ are the charges at the points A, B and O.
Substituting the values of the charges at these points, we have –
$\Rightarrow {V_P} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{q}{{r - a}} - \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{q}{{r + a}} + \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{q}{r}$
Given that $r > > a$, we can say that –
Thus, the above equation becomes –
$\Rightarrow {V_P} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{qa}{r^2} + \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{q}{r}$
Thus, we have obtained the value of electric potential at point P.

Note: If we take a close look at the charge configuration, we see that a charge q is present in midst of a dipole of charge q and distance 2a. Given that the answer is equal to the electric potential of an individual free charge q placed at random in space, we can deduce that the concept that the net electric potential due to the dipole at any point on the dipole axis is equal to zero.