Question

A certain substance A tetramerizes in water to the extent of $80\% $. A solution of $2.5g$ of A in $100g$ of water lowers the freezing point by $0.3^{o}C$. The molar mass of A is:
A. $122$
B. $31$
C. $244$
D. $62$

Answer 1

Hint: In this question, we have to take into account the concept of Van't Hoff Factor as the substance undergoes tetramerization in the question because the extent to which a substance associates or dissociates is described only by Van't Hoff factor.

Complete step by step answer: In this question, the concept of depression of freezing point is used. The freezing point of a substance is defined as the temperature at which the vapour pressure of the substance in its liquid phase is equal to the vapour pressure in solid phase. This means that a solution will freeze when its vapour pressure becomes equals to the vapour pressure of pure solid solvent. According to Raoult’s law, when a non-volatile solute is added to the solvent, its vapour pressure decreases and now it would become equal to that of solid solvent at lower temperature. Thus, the freezing point of the solvent decreases.

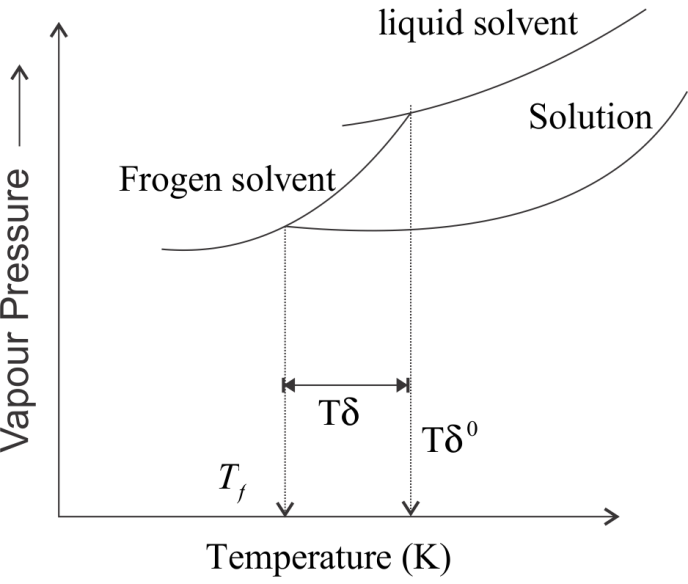
Let $T_f^{o} $ be the freezing point of pure solvent and ${T_f}$ be its freezing point when non-volatile solute is dissolved in it. The decrease in freezing point i.e. $\Delta {T_f} = T_f^{o} - {T_f}$ is known as depression of freezing point.
Depression of freezing point $\left( {\Delta {{\rm T}_f}} \right)$ for dilute solution is directly proportional to molality $m$ of the solution.
i.e. $\Delta {T_f} \propto m{\text{ }}or{\text{ }}\Delta {T_f} = {K_f} \cdot m$
${K_f}$ is a constant known as the molal constant of cryoscopic constant.
Now, according to the question, a substance tetramerizes in water i.e. in this question we have to take the concept of Van't Hoff Factor (i). Van't Hoff Factor gives the extent of dissociation or association of a substance. Since the substance tetramerizes (association), so the value of i can be calculated as $i = 1 - \propto + \dfrac{ \propto }{n}$ ….. (i)
Here, n becomes $4$. Since the extent of association is $80\% $, means that value of $ \propto $ becomes $80\% $ of $1 = 0.8$. Thus putting all values in equation (i) , we get
$i = 1 - 0.8 + \dfrac{{0.8}}{4} = 0.2 + 0.2 = 0.4$
$i = 0.4$
Now, the value of depression of freezing point $\left( {\Delta {T_f}} \right)$ is $0.3^{o}C$ and value of ${K_f}$ as we know for water is $1.86Kg{\text{ }}K{\text{ }}mo{l^{ - 1}}$.
Now, putting all the values in equation: $\Delta {T_f} = i \cdot {K_f} \cdot m$
We get, $0.3 = 0.4 \times 1.86 \times m$ ……………. (ii)
As we know molality is no. of moles of substance present per kg of solvent and is calculate by using $m = \dfrac{{{\text{given mass of substance}}}}{{{\text{molar mass of substance}}}} \times \dfrac{{1000}}{{{\text{weight of solvent}}\left( g \right)}}$
Now, the mass of the substance given is $2.5g$ and the weight of solvent is $100g$. Thus molality becomes $m = \dfrac{{2.5g}}{{{\text{molar mass of substance}}}} \times \dfrac{{1000}}{{100}}$ ……………… (iii)
Now, putting equation (iii) in equation (ii), we get
$\Rightarrow$ $0.3 = 0.4 \times 1.86 \times \dfrac{{2.5}}{{{\text{molar mass of solvent}}}} \times \dfrac{{1000}}{{100}}$
Or, molar mass of substance $ = \dfrac{{0.4 \times 1.86 \times 2.5 \times 1000}}{{0.3 \times 100}} = 62g$
Hence, the molar mass of the substance is $62g$
So, the correct answer is “Option D”.

Note: Since the association or dissociation completely is represented by $1$. So the $80\% $ association is represented by $80\% $ of $1 = 0.80$. Moreover, the depression in freezing point is used in melting of ice on roads by using $NaCl$. It is also used as a concept of antifreeze solution.