Question

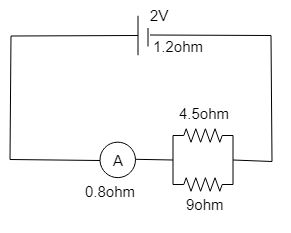
A cell of emf $2V$ and internal resistance of $1.2\Omega $ is connected with an ammeter of resistance $0.8\Omega $ and two resistors of $4.5\Omega $ and $9\Omega $ as shown in the diagram:
(i) What would be the reading on the Ammeter?
(ii) What is the potential difference across the terminals of the cell?

Answer 1

Hint:First we need to find the value of the equivalent resistance in order to solve this question. The two resistors of $4.5\Omega $ and $9\Omega $ are in a parallel combination and their resultant is in series with the resistance of $0.8\Omega $. By applying this concept, we are able to solve this question.

Complete step by step answer:
Given, EMF of this circuit $E = 2V$. Internal resistance of the cell $r = 1.2\Omega $. Let us consider the external resistance to be $R$. Since two resistors of $4.5\Omega $ and $9\Omega $ are connected in a parallel circuit. So, the equivalent resistance of these two resistors is,
$\dfrac{1}{{{R_p}}} = \dfrac{1}{{4.5}} + \dfrac{1}{9}$

On taking the LCM,
$\dfrac{1}{{{R_p}}} = \dfrac{{2 + 1}}{9}$
$\Rightarrow \dfrac{1}{{{R_p}}} = \dfrac{3}{9}$
On further simplifying, we get,
$\dfrac{1}{{{R_p}}} = \dfrac{1}{3}$
$\Rightarrow {R_p} = 3\Omega $
Now, the resistance of $0.8\Omega $ and ${R_p} = 3\Omega $ are in series combination. So,
$R = 3 + 0.8$
$\Rightarrow R = 3.8\Omega $

(i) The value of the current in the resistance of $0.8\Omega $ is given by,
$I = \dfrac{E}{{R + r}}$
On putting the required values, we get,
$I = \dfrac{2}{{3.8 + 1.2}}$
$\Rightarrow I = \dfrac{2}{5}$
$\Rightarrow I = 0.4A$

So, the value of the current in the resistance of $0.8\Omega $ is $I = 0.4\,A$.

(ii) The potential difference across the terminals of the cell is,
$V = E - Ir$
On putting the required values, we get,
$V = 2 - (0.4 \times 1.2)$
$\Rightarrow V = 2 - 0.48$
$\therefore V = 1.52V$

So, the potential difference across the terminals of the cell is $V = 1.52\,V$.

Note:Internal Resistance is defined as the resistance which acts in the battery. This resistance resists the current flow when the battery is connected to a circuit. The reason that the batteries have an internal resistance is because the elements that make a battery are not perfect conductors. An ideal batter must have no resistance but an ideal battery is hypothetical.