Question

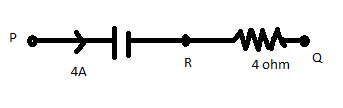
A cell has terminal voltage $2V$ in open circuit and internal resistance of the given cell is $2\Omega $. If $4A$ of current is flowing between points $P$ and $Q$ in the circuit and then the potential difference between $P$ and $Q$ is

A. $22V$
B. $24V$
C. $30V$
D. $26V$

Answer 1

Hint:
Here we have to find the potential difference between the batteries in each terminal and compare them to find the potential difference between $P$ and $Q$.

First let us see what potential difference is-
The potential difference is the difference between two points in a circuit in the amount of energy that the charge carriers have.
Terminal potential difference- Terminal potential difference is usually found in cells or batteries.
The potential difference in a closed circuit between the two poles of a cell is called the cell’s terminal potential difference. When we measure the battery’s emf as we evaluate the potential difference between the terminals of a battery that is not a full circuit. This is the overall amount of work the battery can do to push charge from one terminal through the circuit to the other terminal per coulomb of charge.
Terminal voltage is mathematically represented by-
$V = emf - Ir$
   where $emf$ is the electromotive force,
   $I$ is the current flowing, and
   $r$ is the resistance.

Complete step by step solution-
Given,
A cell has terminal voltage $2V$ in open circuit and internal resistance of the given cell is $2\Omega $
$4A$ of current is flowing between points $P$ and $Q$ in the circuit

$
  E = 2V \\
  I = 4A \\
  r = 4\Omega \\
 $
The potential difference between $P$ and $Q$ =?
Case 1
Terminal potential difference
$ = {V_P} - {V_R} = E + Ir = 2 + (4 \times 2) = 10V$
               ...... (1)
Case 2
Terminal potential difference
 $ = {V_R} - {V_Q} = Ir = 4 \times 4 = 16V$
               ...... (2)
From equation (1) and (2), we get-
$
  {V_P} - {V_R} + {V_R} - {V_Q} \\
   = 10 + 16 \\
  {V_P} - {V_Q} = 26V \\
 $

Hence, the potential difference between $P$ and $Q$ is $26V$

Note:
Here as we can see from case (2) we have not added any emf with the second equation. It is because there is no induced emf in the terminal between $R$ and $Q$.