Question

A Cathedral window is built in the shape of a semicircle. If the window is to contain three stained glass sections of equal size, what is the area of each stained glass section? Express the answer to the nearest square foot.

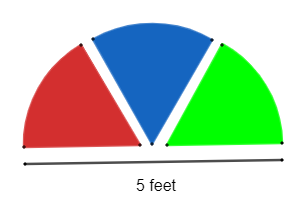
(a) 1 sq. ft.
(b) 3 sq. ft.
(c) 13 sq. ft.
(d) 26 sq. ft.

Answer 1

Hint: First find the radius from the given diameter and then find the area of the cathedral window by using the formula \[A=\dfrac{\pi {{r}^{2}}}{2}\]. Area of each stained glass section is equal therefore divide the area of the cathedral window by the no. of stained glass sections to find the final answer.

Complete step by step solution:
The diameter \[d\] of the given semicircle is 5 ft.
We know the formula to find the radius with the diameter is expressed as,
 \[r=\dfrac{d}{2}\]
Applying the above formula to find the radius of the semicircle,
\[r=\dfrac{5}{2}\]
\[r=2.5\]

We know the area \[A\] of a semicircle with radius \[r\] can be written as,
 \[A=\dfrac{\pi {{r}^{2}}}{2}\]
Applying the above formula the area of semicircle with radius r = 2.5 is,
\[A=\dfrac{\pi {{\left( 2.5 \right)}^{2}}}{2}\]
Squaring the radius in the equation,
\[A=\dfrac{\pi \left( 6.25 \right)}{2}\]
Substituting the value of \[\pi \] in the equation,
\[A=\dfrac{6.25\times 3.141592}{2}\]
On Multiplying the value of \[\pi \] with 6.25 we get,
\[A=\dfrac{19.63495}{2}\]
Dividing 19.63495 by 2 to get the area of the semicircle,
\[A=9.817475\]
The area of each stained glass section \[Ar\] which are contained in the cathedral window can be expressed as division of area of the cathedral window by 3.
\[Ar=\dfrac{A}{3}\]
Applying the above relation and substituting the value \[A=9.817475\] we get,
\[Ar=\dfrac{9.817475}{3}\]
Dividing 9.817475 by 3 to get the area of each stained glass,
\[Ar=3.27\]
Approximating the area of each stained glass section to the nearest sq. ft. we get,
\[Ar=3\]
We have obtained the area as 3 sq. ft.
Hence option (b) is the correct answer.

Note: The area of the stained glass section can also be calculated by finding the angle of each sector, as all the sectors subtend equal angles at the center and the sum of all the angles subtended by the sectors is \[180{}^\circ \]. The value of angle \[\theta \] can be calculated as \[\dfrac{180}{3}=60{}^\circ \].The area of the sector with angle \[\theta \] is given by the formula \[A=\dfrac{\theta }{360{}^\circ }\times \pi {{r}^{2}}\]. Apply this formula to find the area of each stained glass section.