Question

A carpenter makes stools for electricians with a square top of side 0.5m and at a height of 1.5m meter above ground. Also, each leg is inclined at an angle of 60 degrees to the ground. Find the length of each leg and also two steps to be put at equal distances.

Answer 1

Hint: First we will draw the required figure and with the help of that we will use trigonometric formulas like $\sin 60=\dfrac{height}{hypotenuse}$ and $\tan 60=\dfrac{height}{base}$ on the required triangle to find the value of length of each leg by using all the values that is given and after that we have to find the length of the two steps from the smaller triangle like DKG and DLI.

Complete step-by-step answer:
Let’s first draw the diagram,

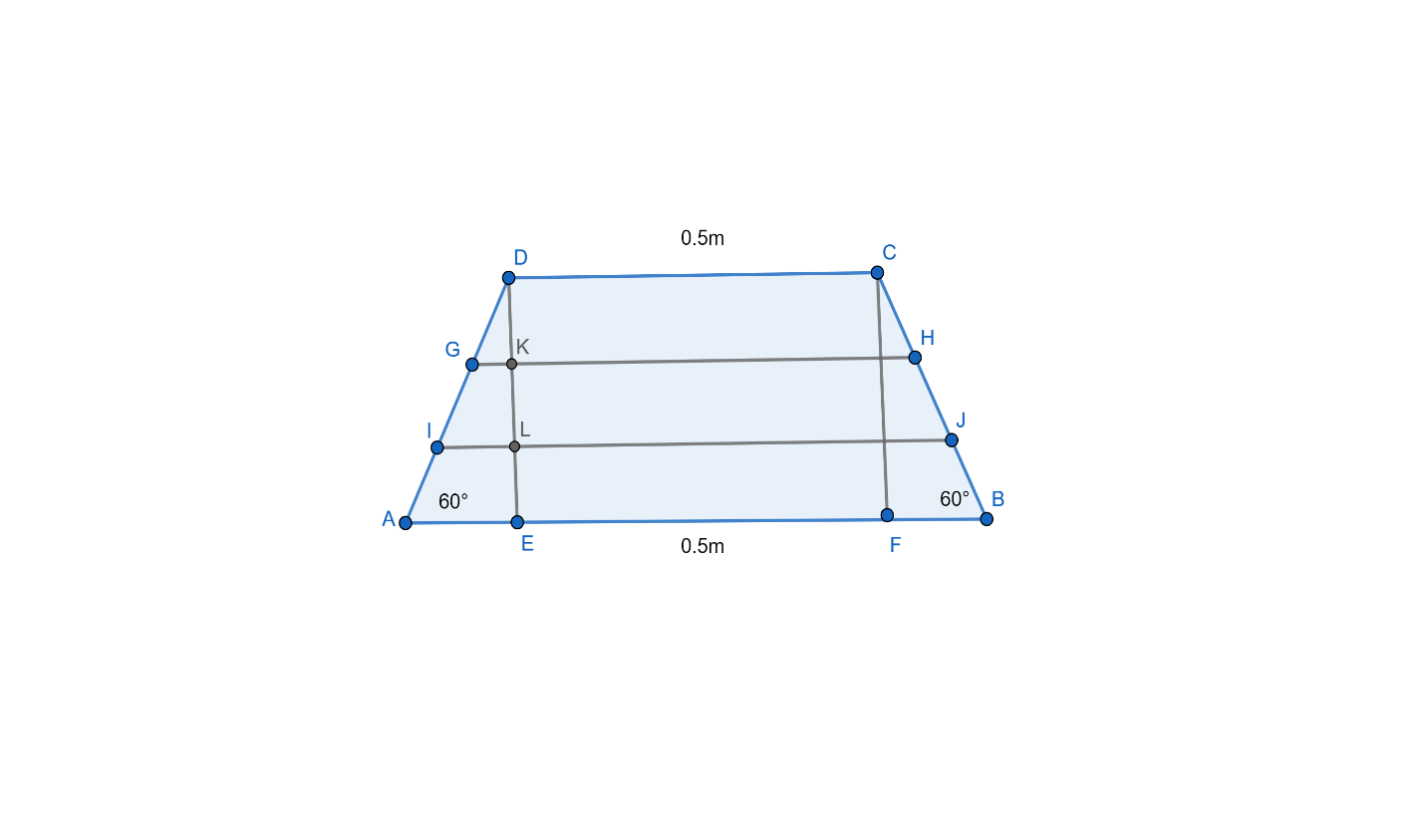
In the above diagram, we can see that
AD = BC = length of leg
The two steps are GH and IJ.
$\begin{align}
  & \angle DGK=60 \\
 & \angle DIL=60 \\
\end{align}$
DK = KL = LE = 0.5m
CF = DE = 1.5m
Now let’s first find the length of leg AD,
In triangle ADE, height = DE and hypotenuse = AD
Now we get,
$\sin 60=\dfrac{height}{hypotenuse}$
Substituting the values of height and hypotenuse we get,
$\begin{align}
  & \Rightarrow \sin 60=\dfrac{DE}{AD} \\
 & \Rightarrow \dfrac{\sqrt{3}}{2}=\dfrac{1.5}{AD} \\
 & \Rightarrow AD=\dfrac{3}{\sqrt{3}}=\sqrt{3} \\
\end{align}$
Hence, the length of each leg = $\sqrt{3}m$
Now we will find the value of step GH,
The two triangles ADE and BCF are the same, so if we find the length on one side the other will be the same.
In triangle DGK, height = DK = 0.5m and base = GK.
$\tan 60=\dfrac{height}{base}$
Substituting the values of height and base we get,
$\begin{align}
  & \tan 60=\dfrac{0.5}{GK} \\
 & GK=\dfrac{0.5}{\tan 60} \\
 & GK=\dfrac{1}{2\sqrt{3}}=0.288 \\
\end{align}$
The length of the step GH will be,
= 2GK + 0.5
= 1.076m
Now we will find the value of step IJ,
The two triangles ADE and BCF are the same, so if we find the length on one side the other will be the same.
In triangle DIL, height = DL = 1m and base = IL.
$\tan 60=\dfrac{height}{base}$
Substituting the values of height and base we get,
$\begin{align}
  & \tan 60=\dfrac{1}{IL} \\
 & IL=\dfrac{1}{\tan 60} \\
 & IL=\dfrac{1}{\sqrt{3}}=0.577 \\
\end{align}$
The length of the step IJ will be,
= 2IL + 0.5
= 1.654m
Hence, we have found all the required values.

Note: In this the figure that we have constructed is very important without that it would be very difficult for anyone to solve this question. And the formulas that we have used are also important. One can also solve this question by taking the right side triangles like BCF and use the same formula to find the answer.