Question

A Carnot engine absorbs $750\;J$ of heat energy from a reservoir at $137^{\circ}C$ and rejects $500\;J$ of heat during each cycle. Then the temperature of the sink is:
A. $0.25^{\circ}C$
B. $0.34^{\circ}C$
C. $0.44^{\circ}C$
D. $0.54^{\circ}C$

Answer 1

Hint: Recall that a Carnot engine transfers heat from a warm region to a cool region via a working fluid that determines the efficiency of the engine. The efficiency of the engine is expressed as the ratio of work done by the working fluid to the heat incident on the working fluid. It is also given in a similar way with respect to the temperature of the source and sink. Use this to obtain a relation between the heat transferred and the temperature of the reservoirs and plug in the values to get the desired result.
Formula Used:
Efficiency of Carnot engine: $\nu = 1-\dfrac{T_C}{T_H} = 1- \dfrac{Q_C}{Q_H}$

Complete step by step answer:
Let us begin by establishing a brief understanding of what a Carnot engine is.
A Carnot engine is a theoretical heat engine where the engine transfers energy from a hot region to a cold region of space, and in the process converts some of that energy into mechanical work. The essence of a Carnot engine is that it constrains the maximum efficiency that any heat engine can possess.

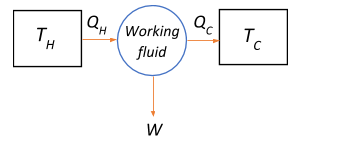
From the block diagram, assuming that $T_H>T_C$, heat flows from the hot region $T_H$, called the source, to the cool region $T_C$ called the sink. The heat engine transfers $Q_H$ amount of heat from the source to the sink $Q_C$, through a working fluid which absorbs a part of the heat $Q_H -Q_C$
Thus, for the Carnot engine we are given $T_H = 137 +273 = 410K$, $Q_H = 750\;J$.
And since the working fluid rejects $500\;J$ of heat, $Q_C = 500\;J $
Now, the efficiency of a Carnot engine is given as:
$\nu = 1 - \dfrac{Q_C}{Q_{H}}$ and $\nu = 1- \dfrac{T_C}{T_H}$ in terms of the heat transferred and temperature respectively. Since every Carnot heat engine between a pair of heat reservoirs is equally efficient regardless of the working fluid employed (Carnot’s theorem):
$1 - \dfrac{Q_C}{Q_{H}} = 1- \dfrac{T_C}{T_H}$
$\Rightarrow \dfrac{T_C}{T_H}=\dfrac{Q_C}{Q_H}$
$\Rightarrow \dfrac{T_C}{410} = \dfrac{500}{750}$
$\Rightarrow T_C = \dfrac{500 \times 410}{750} = 273.34K = (273.34-273)^{\circ}C = 0.34^{\circ}C$
Therefore, the temperature of the sink is found to be B. $0.34^{\circ}C$

Note:
Remember that a Carnot engine works in a 4-step cycle, contrary to the modern approach that we have discussed in the question for our convenience. It involves isothermal expansion, adiabatic expansion, isothermal compression and adiabatic compression respectively, all of which are reversible processes. On a reverse cycle, the heat engine functions as a heat pump.
Also, do not forget that the efficiency of an irreversible heat engine is always less than that of a reversible heat engine. Practical engine cycles are irreversible and consequently have a relatively lower efficiency than the Carnot efficiency.