Question

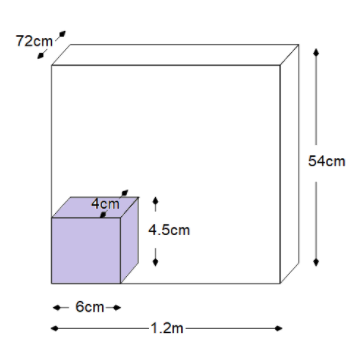
A cardboard box is \[1.2\,m\] long , \[72\,cm\] wide and \[54\,cm\] high. How many bars of soap can be put into it if each bar measures \[6\,cm \times 4.5\,cm \times 4\,cm\] ?

Answer 1

Hint:In order to solve this question first, we make all the sides of both box and bar in the same unit so we are converting them into centimeters. Then we know that the bar has some volume and the box has some volume so the bar is placed in a box and occupies some volume. Then we assume that the number of bars put into cardboard boxes. Then we multiply that number with the volume of the bar and equate that to the volume of cardboard and on rearranging and doing calculations we find the number of bars put into a box.

Complete step by step answer:
Given: Side of cardboard box in same unit - \[120\,cm\] long , \[72\,cm\] wide and \[54\,cm\] .
Sid of the bar in the same unit- \[6\,cm \times 4.5\,cm \times 4\,cm\].
To find-

Number of bars put into cardboard. We know that bar is put inside the box and covers some space. So we equate the multiplication of a number of bars and volume of the bar to the volume of a cardboard box.Let, the number of bars put into the box is \[x\].
\[x \times \text{volume of bar = volume of cardboard box}\]

On using the formula of volume of cuboid.
\[x \times 6\,cm \times 4.5\,cm \times 4\,cm = 120\,cm \times 72\,cm \times 54\,cm\]
On canceling the unit from both sides and rearranging.
\[x = \dfrac{{120\,cm \times 72\,cm \times 54\,cm}}{{6\,cm \times 4.5\,cm \times 4\,cm}}\]
On multiplying the numbers.
\[x = \dfrac{{466560}}{{108}}\]
On dividing the number we get a number of bars that are put into a box.
\[\therefore x = 4320\]

Therefore, the number of bars inside the cardboard box is 4320.

Note:Although this question is easy, students must know the concept of why we equate volume of both the objects. Students often make mistakes like they will not convert all sides of the object to the same unit. The question may be asked in such a way that we have to fix tiles in the ground of some area and some areas of tile are given then we equate the area of both ground and number of tiles.