Question

A car wiper has two blades each of length 56 cm. How much area will they both sweep if each makes an angle of 135° while it moves. $ \left( {\pi = \dfrac{{22}}{7}} \right) $

Answer 1

Hint: The diagram can be drawn showing the rea swept by wipers at the given angles and observed. They will make a sector whose area can be calculated as:
 $ \dfrac{\theta }{{360}} \times \pi {r^2} $ where,

 $ \theta $ = angle formed at the centre
r = radius of the formed circle.
As the wipers are 2 in number, the required area will be:
 $ 2 \times \dfrac{\theta }{{360}} \times \pi {r^2} $

Complete step-by-step answer:
The diagram of the wipers sweeping the area :

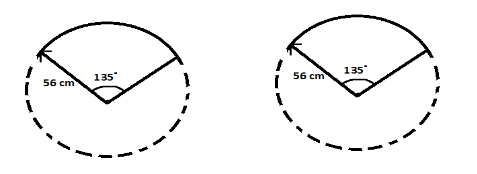
The area covered by the wipers at a certain angle forms a sector of a circle.
The area of a sector is:
 $ \dfrac{\theta }{{360}} \times \pi {r^2} $ , here
The angle formed at the centre $ \left( \theta \right) $ = 135°
Radius (r) = Length of the wiper = 56 cm
Substituting the values:
 $ \dfrac{{135}}{{360}} \times \dfrac{{22}}{7} \times {(56)^2} $ $ \left( {\because \pi = \dfrac{{22}}{7}} \right) $
We have two wipers, so this area will be multiplied by 2 to obtain the total wiped area (A).
 $\Rightarrow A = 2 \times \dfrac{{135}}{{360}} \times \dfrac{{22}}{7} \times {(56)^2} $
A = 7392
As the length of the wiper is in cm, the area swept will be in $ c{m^2} $
A = 7392 $ c{m^2} $
Therefore, the area that both the wipers will sweep is 7392 $ c{m^2} $

Note: A sector is that portion of a circle which is enclosed by two radii and an arc.
In general, a circle can be divided into sectors as: minor sector (enclosing lesser area) and major sector (enclosing comparatively more area).
A sector has area $ \dfrac{\theta }{{360}} \times \pi {r^2} $ because:
Angle formed by a sector is say $ \theta $
Angle formed by a sector is 360°
Area of circle = $ \pi {r^2} $
Then, the area of the sector is given by the product of the area of circle and angle formed by the sector divided by that formed by the circle.