Question

A car weighing 100 kg is on a slope that makes an angle ${30^ \circ }$with the horizontal. The component of car’s weight parallel to the slope is ($g = 10m{s^{ - 2}}$)
A. 500 N
B. 1000 N
C. 15000 N
D. 20000 N

Answer 1

Hint:There are two kinds of quantities: Scalar and Vector. Scalar quantities are expressed only in terms of magnitude, for example, speed, time, temperature, mass. Vector quantities are expressed in magnitude as well as direction, for example, velocity, force, acceleration, electric field.

Complete step-by-step answer:
Consider a car of mass 100 kg on a slope that makes an angle of ${30^ \circ }$ as shown:

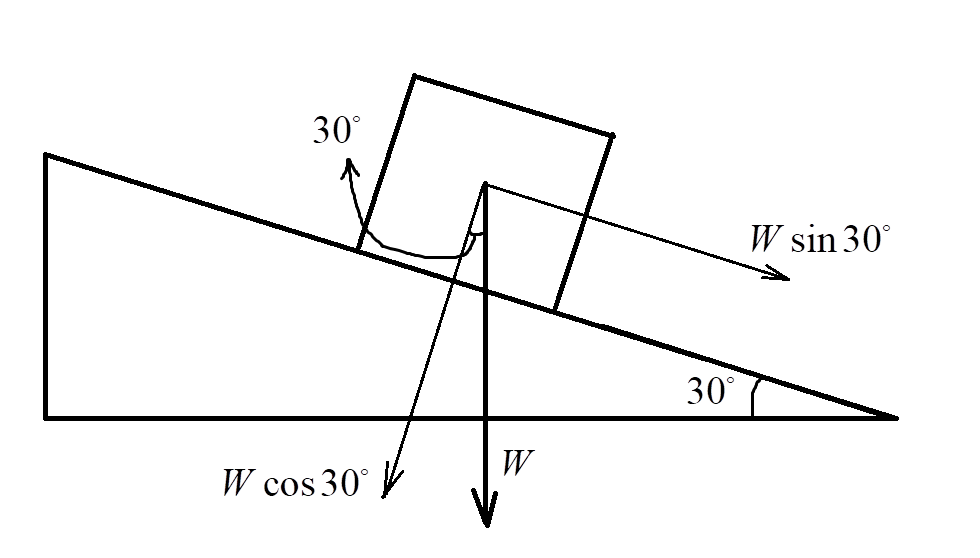
The weight of the car, which is 100 kg, acts vertically in the downward direction as shown.
Since, the weight (or force) is a vector, it can be resolved into 2 components: One horizontal and one vertical component as shown.
If we resolve the weight into 2 components, we have: $W\cos {30^ \circ }$and $W\sin {30^ \circ }$ as shown in the dotted lines in the above figure.

The weight, W = mg
Given,
Mass, m = 100 kg
Acceleration due to gravity, $g = 10m{s^{ - 2}}$
The weight, W = mg = $100 \times 10 = 1000N$
In the problem, they have asked the component of the car’s weight that is parallel to the slope. In this case, we can see that the component of force parallel to the slope is $\sin \theta $.
Hence, the component is, $W\sin {30^ \circ } = W \times \dfrac{1}{2} = 1000 \times \dfrac{1}{2} = 500N$

Hence, the correct option is Option A.

Note: Students generally confuse while writing the horizontal and vertical components of a vector. You can use a simple and handy thumb rule as shown here:

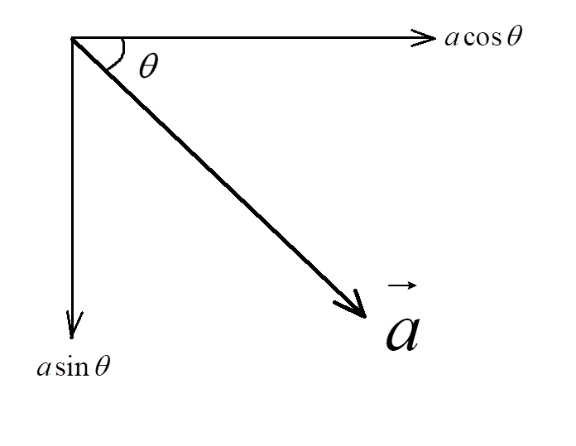
Consider a vector $\vec a$ inclined at angle $\theta $ as shown in the above figure: - The line that is attached to the angle $\theta $ is designated as $\cos \theta $. - The other line that is not attached to the angle$\theta $ is designated as $\sin \theta $ .