
A car travels from P to Q at a constant speed. If the speed were increased by $10$ km/hr, it would have taken $1$ hour less to cover the distance. It would have taken further $45$ minutes lesser if the speed was further increased by $10$ km/hr. What is the distance between the two cities?
Answer
584.4k+ views
Hint: Let the time for traveling at a constant speed from P to Q be \[\dfrac{{\text{x}}}{{\text{y}}}\] where x be the distance and y be the speed. Now if the speed was increased by $10$ km/hr then the time will be $\dfrac{{\text{x}}}{{{\text{y + 10}}}}$ and since it would have taken $1$ hour less then \[\dfrac{{\text{x}}}{{\text{y}}} - \dfrac{{\text{x}}}{{{\text{y + 10}}}} = 1\]. Simplify it and form an equation. Form another equation by following the same process for when speed is increased further by $10$ km/hr. Solve the equations to find the value of x.
Complete step-by-step answer:
Given, a car travels from city P to Q at a constant speed. Let the distance be x m and speed be y km/hr. Then the time taken will be=$\dfrac{{{\text{distance}}}}{{{\text{speed}}}} = \dfrac{{\text{x}}}{{\text{y}}}$
Now if the speed was increased by $10$ km/hr, it. So the time taken will be $\dfrac{{\text{x}}}{{{\text{y + 10}}}}$.Since it would have taken $1$ hour lesser to cover the distance, then
$ \Rightarrow $ $\dfrac{{\text{x}}}{{\text{y}}} - 1 = \dfrac{{\text{x}}}{{{\text{y + 10}}}}$ $ \Rightarrow \dfrac{{\text{x}}}{{\text{y}}} - \dfrac{{\text{x}}}{{{\text{y + 10}}}} = 1$
On simplifying the equation we get,
$ \Rightarrow \dfrac{{{\text{xy + 10x - xy}}}}{{{\text{y(y + 10)}}}} = 1 \Rightarrow 10{\text{x = }}{{\text{y}}^2} + 10{\text{y}}$
$ \Rightarrow {{\text{y}}^2}{\text{ + 10y - 10x = 0}}$ ---- (i)
Now if the speed is further increased by $10$ km/hr then the total speed will be ${\text{y + 20}}$ km/hr. The time will be further decreased by $45$ minutes, so the lesser time will be $1{\text{hr45min}}$.
$1{\text{hr45min}}$$ = 1 + \dfrac{{45}}{{60}} = 1 + \dfrac{9}{{12}} = \dfrac{{21}}{{12}} = \dfrac{7}{4}{\text{hrs}}$
So then according to question,
$ \Rightarrow \dfrac{{\text{x}}}{{\text{y}}} - \dfrac{{\text{x}}}{{{\text{y + 20}}}} = \dfrac{7}{4} \Rightarrow \dfrac{{{\text{xy + 20x - xy}}}}{{{{\text{y}}^2}{\text{ + 20y}}}} = \dfrac{7}{4}$
On simplifying we get,
$ \Rightarrow 80{\text{x = 7}}{{\text{y}}^2}{\text{ + 140y}} \Rightarrow {\text{7}}{{\text{y}}^2}{\text{ + 140y - }}80{\text{x = 0}}$ --- (ii)
On putting the value of x from eq. (i) into (ii) we get,
$ \Rightarrow {\text{7}}{{\text{y}}^2}{\text{ + 140y - }}80\left( {\dfrac{{{{\text{y}}^2}{\text{ + 10y}}}}{{10}}} \right){\text{ = 0}}$
$ \Rightarrow {\text{7}}{{\text{y}}^2}{\text{ + 140y - }}8{{\text{y}}^2}{\text{ - 80y = 0}}$
$ \Rightarrow - {{\text{y}}^2}{\text{ + 60y - = 0}} \Rightarrow {{\text{y}}^2}{\text{ = 60y}}$
$ \Rightarrow $ ${\text{y = 60}}$
On putting the value of y in eq.(i) we get,
$ \Rightarrow {60^2}{\text{ + 10}} \times {\text{60 - 10x = 0}} \Rightarrow {\text{3600 + 600 - 10x = 0}}$
$ \Rightarrow 10{\text{x = 4200}} \Rightarrow {\text{x = }}\dfrac{{4200}}{{10}} = 420$ Km
Hence the distance between the 2 cities is $420$ km.
Note: The question can also be solved by this method-
We know that distance (d) = speed(s) × time (t) and we have to find the distance (d) in the given question. Since when speed (s) is increased by 10 the time (t) is decreased by 1 hour. Now in the second statement it says that when speed is increased by 20 the time is decreased by 45 minutes which can be written as 7/4hours, then we can write the coefficients of s and t as
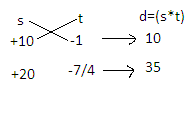
We can cross multiply the coefficients of s and t to form the equation. So the equations will be $ - {\text{s + 10t = 10 and - }}\dfrac{7}{4}{\text{s + 20t = 35}}$. On solving these eq., we get ${\text{t = 7hrs and s = 60km/hr}}$.Now put the values in the formula of distance and you’ll get the answer.
Complete step-by-step answer:
Given, a car travels from city P to Q at a constant speed. Let the distance be x m and speed be y km/hr. Then the time taken will be=$\dfrac{{{\text{distance}}}}{{{\text{speed}}}} = \dfrac{{\text{x}}}{{\text{y}}}$
Now if the speed was increased by $10$ km/hr, it. So the time taken will be $\dfrac{{\text{x}}}{{{\text{y + 10}}}}$.Since it would have taken $1$ hour lesser to cover the distance, then
$ \Rightarrow $ $\dfrac{{\text{x}}}{{\text{y}}} - 1 = \dfrac{{\text{x}}}{{{\text{y + 10}}}}$ $ \Rightarrow \dfrac{{\text{x}}}{{\text{y}}} - \dfrac{{\text{x}}}{{{\text{y + 10}}}} = 1$
On simplifying the equation we get,
$ \Rightarrow \dfrac{{{\text{xy + 10x - xy}}}}{{{\text{y(y + 10)}}}} = 1 \Rightarrow 10{\text{x = }}{{\text{y}}^2} + 10{\text{y}}$
$ \Rightarrow {{\text{y}}^2}{\text{ + 10y - 10x = 0}}$ ---- (i)
Now if the speed is further increased by $10$ km/hr then the total speed will be ${\text{y + 20}}$ km/hr. The time will be further decreased by $45$ minutes, so the lesser time will be $1{\text{hr45min}}$.
$1{\text{hr45min}}$$ = 1 + \dfrac{{45}}{{60}} = 1 + \dfrac{9}{{12}} = \dfrac{{21}}{{12}} = \dfrac{7}{4}{\text{hrs}}$
So then according to question,
$ \Rightarrow \dfrac{{\text{x}}}{{\text{y}}} - \dfrac{{\text{x}}}{{{\text{y + 20}}}} = \dfrac{7}{4} \Rightarrow \dfrac{{{\text{xy + 20x - xy}}}}{{{{\text{y}}^2}{\text{ + 20y}}}} = \dfrac{7}{4}$
On simplifying we get,
$ \Rightarrow 80{\text{x = 7}}{{\text{y}}^2}{\text{ + 140y}} \Rightarrow {\text{7}}{{\text{y}}^2}{\text{ + 140y - }}80{\text{x = 0}}$ --- (ii)
On putting the value of x from eq. (i) into (ii) we get,
$ \Rightarrow {\text{7}}{{\text{y}}^2}{\text{ + 140y - }}80\left( {\dfrac{{{{\text{y}}^2}{\text{ + 10y}}}}{{10}}} \right){\text{ = 0}}$
$ \Rightarrow {\text{7}}{{\text{y}}^2}{\text{ + 140y - }}8{{\text{y}}^2}{\text{ - 80y = 0}}$
$ \Rightarrow - {{\text{y}}^2}{\text{ + 60y - = 0}} \Rightarrow {{\text{y}}^2}{\text{ = 60y}}$
$ \Rightarrow $ ${\text{y = 60}}$
On putting the value of y in eq.(i) we get,
$ \Rightarrow {60^2}{\text{ + 10}} \times {\text{60 - 10x = 0}} \Rightarrow {\text{3600 + 600 - 10x = 0}}$
$ \Rightarrow 10{\text{x = 4200}} \Rightarrow {\text{x = }}\dfrac{{4200}}{{10}} = 420$ Km
Hence the distance between the 2 cities is $420$ km.
Note: The question can also be solved by this method-
We know that distance (d) = speed(s) × time (t) and we have to find the distance (d) in the given question. Since when speed (s) is increased by 10 the time (t) is decreased by 1 hour. Now in the second statement it says that when speed is increased by 20 the time is decreased by 45 minutes which can be written as 7/4hours, then we can write the coefficients of s and t as
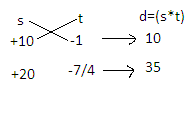
We can cross multiply the coefficients of s and t to form the equation. So the equations will be $ - {\text{s + 10t = 10 and - }}\dfrac{7}{4}{\text{s + 20t = 35}}$. On solving these eq., we get ${\text{t = 7hrs and s = 60km/hr}}$.Now put the values in the formula of distance and you’ll get the answer.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Complete reduction of benzene diazonium chloride with class 12 chemistry CBSE

How can you identify optical isomers class 12 chemistry CBSE

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

What are the 12 elements of nature class 8 chemistry CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Convert 40circ C to Fahrenheit A 104circ F B 107circ class 8 maths CBSE

Advantages and disadvantages of science




