Question

A car sometimes overturns while taking a turn. When it overturns, it is
A. the inner wheel that leaves the ground first
B. the outer wheel which leaves the ground first
C. both the wheels leaves the ground simultaneously
D. either wheel which leaves the ground first

Answer 1

Hint: Overturning occurs on roads when the car tries to change directions by making sharp turns. It often occurs in the case of vehicles whose center of gravity is higher from the surface of roads.

Complete step by step answer:

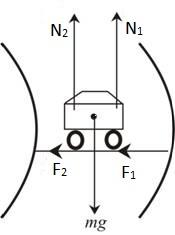
Consider a car moving in a straight line and it suddenly takes a sharp turn towards the right. Now the upper portion of the car still tends to go in the straight path due to inertia i.e., according to Newton’s first law of motion. But the lower portion starts moving right because the driving wheel has been turned accordingly. If the inertial force on the upper portion is higher, it provides torque on the car’s center of gravity so that it overturns.

The overturning will always take place by lifting off the inner wheels from the ground on the curved path.

The limiting case for a four-wheeler to begin overturn is given as:
Let us consider weight of the object to be Mg
‘N’ is the total normal reaction, ‘F’ is the total friction force and ‘G’ is the center of gravity.
If ‘v’ is the velocity and ‘r’ is the radius, then the distance between the wheels can be written as 2a.
The frictional force provides the necessary centripetal force

$F=\dfrac{m{{v}^{2}}}{r}$
At the beginning of overturn, the inner wheels will lift off from the ground. The pressure on the ground due to inner wheels will become zero and so the normal reaction on inner wheels is zero.

${{N}_{1}}+{{N}_{2}}=0+{{N}_{2}}={{N}_{2}}=mg$

On considering the center of gravity,

${{N}_{2}}\times a=F\times h$

Substituting the values in above equation, we get

$mg\times a=\dfrac{m{{v}^{2}}}{r}\times h$ or
${{V}_{\max }}=\dfrac{\sqrt{rga}}{h}$

If the speed goes beyond the maximum velocity, overturning takes place.
Therefore, the correct answer for the given question is option (A).

Note: The radius of the turn of the inner wheel is less than the radius of turn of the outer wheel, so the maximum speed of the inner wheel is also less than that of the outer wheel which makes the inner wheel to leave the ground first.