Question

A car slows down uniformly from a speed of 21.0${m}/{s}\;$ to rest in 6.00 sec. How far did it travel in that time?

Answer 1

Hint: The car is slowing down from a speed of 21.0${m}/{s}\;$ to rest (0.00${m}/{s}\;$) in 6.00 sec which means the acceleration of car is negative, so by calculating acceleration and using third equation of motion we can calculate total distance traveled before coming to rest.

Formula used:
${{U}^{2}}_{f}-{{U}^{2}}_{i}=2aS$

Complete Step by step solution:

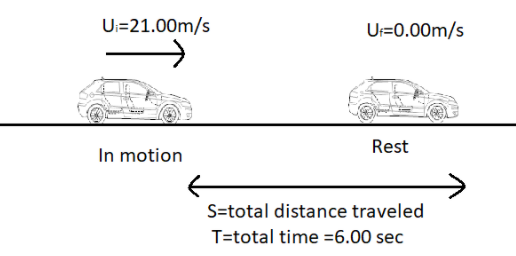
Initial speed ${{U}_{i}}$=21.0${m}/{s}\;$,
Final speed ${{U}_{f}}$=0.00${m}/{s}\;$,
Time taken $T$= 6.00 sec,

So, acceleration $a=\dfrac{{{U}_{f}}-{{U}_{i}}}{T}=\dfrac{0.00-21.00}{6.00}=-3.5{m}/{{{s}^{2}}}\;$

Now, by using third equation of motion we have,
${{U}^{2}}_{f}-{{U}^{2}}_{i}=2aS$
Here, $S$ is distance travel by an object in a given interval of time.

$S=\dfrac{{{U}^{2}}_{f}-{{U}^{2}}_{i}}{2a}=\dfrac{{{\left( 0.00 \right)}^{2}}-{{\left( 21.00 \right)}^{2}}}{2\times \left( -3.5 \right)}=63.0m$

Additional information:
Equations of motion describes the behavior of motion and are used to calculate distance, time, velocity or acceleration of an object. First equation is based on velocity- time as if object having some initial velocity that final velocity must be equal to initial plus the acceleration time of total time, second equation is based on position time where position of an object can be calculated with respect to time and acceleration and the last one is based on position velocity where final velocity depends on acceleration and displacement of an object. The mathematical expression of three equations are
$v=u+at$
$s=ut+\dfrac{1}{2}a{{t}^{2}}$
${{v}^{2}}={{u}^{2}}+2as$
Here, $v$ (final speed), $u$(initial speed), $t$ (total time), $a$ (acceleration) and $s$(distance traveled).

Note:
If we are using the third equation of motion acceleration must be constant (positive or negative), for e.g. in our question acceleration is constant. If not then we can’t apply the equation of motion.