Question

A car of weight W is on an inclined road that rises by 100m over a distance of \[1\text{ }km\] and applies a constant frictional force \[\dfrac{W}{20}\] on the car. While moving uphill on the road at a speed of \[10\text{ }m{{s}^{-1}}\], the car needs power \[P\]. If it needs power \[\dfrac{P}{2}\] while moving downhill at speed \[v\] then value of \[v\] is:
A) \[15\text{ }m{{s}^{-1}}\]
B) \[5\text{ }m{{s}^{-1}}\]
C) \[10\text{ }m{{s}^{-1}}\]
D) \[\text{20 }m{{s}^{-1}}\]

Answer 1

Hint:
Using the method of inclined and plane and block force diagram, we will find the value of the angle of inclination when the car goes up. After that the car will experience two forces: one is the downward hill force and the other is the upward hill force. The upward hill force is downward force added by the frictional force and the downhill force is the downward force subtracted from the frictional force. Hence, plotting them in formulas, we get:
The uphill force as Uphill Force \[\text{= Forc}{{\text{e}}_{\text{downward}}}\text{+Forc}{{\text{e}}_{\text{Friction}}}\]
The downhill force as Downhill Force \[\text{= Forc}{{\text{e}}_{\text{friction}}}-\text{Forc}{{\text{e}}_{\text{Downward}}}\]
After this we use the power formula where the formula is:
\[P=F\times v\]
where \[P\] is the power developed, \[F\] is the force developed due to the weight and friction and \[v\] is the velocity of the car moving on the inclined plane. Now both the downhill power and uphill power are the same, hence after finding the power equate both of them to find the velocity.

Complete step by step solution:
Let us draw an inclined plane where the car is moving on the plane as shown below:
               

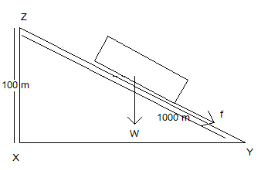
The block is giving a downward force of W and a backward frictional force of f, the distance ZY is given as \[1000m\] and the height XZ is \[100m\].
Now, the angle of inclination of the inclined plane is given as:
\[\sin \theta =\dfrac{100}{1000}\]
\[\Rightarrow \sin \theta =\dfrac{1}{10}\]
Hence, using the values from the question, the value of the frictional force is \[\dfrac{W}{20}\].
So during the uphill force, the force acting due to downward weight (sine component) and the frictional force is drawn downward as:
               

Thereby, the force of the uphill is given as: Uphill Force \[\text{= Forc}{{\text{e}}_{\text{downward}}}\text{+Forc}{{\text{e}}_{\text{Friction}}}\].
The downward force in direction downward and in the same direction as that of the frictional force is \[W\sin \theta \]. Placing the values of \[\text{Forc}{{\text{e}}_{\text{downward}}}=W\sin \theta \] and frictional force as \[\dfrac{W}{20}\ and \sin \theta =\dfrac{1}{10}\].
Uphill Force \[=\text{ }\dfrac{W}{10}+\dfrac{W}{20}\]
\[=\dfrac{3W}{20}\]
Hence, the power developed due to the force and velocity of driving is:
\[P=F\times v\]
Placing the values as found above and in the question, we get the power as:
\[P=\dfrac{3W}{20}\times 10\]
\[=\dfrac{3}{2}W\]
So during the downhill force, the force acting due to downward weight (sine component) and the frictional force is drawn as:
               

Thereby, the force of the downhill is given as: Downhill Force \[\text{= Forc}{{\text{e}}_{\text{friction}}}-\text{Forc}{{\text{e}}_{\text{Downward}}}\]
The downward force in direction downward and in opposite direction as that of the frictional force is \[W\sin \theta \]. Placing the values of \[\text{Forc}{{\text{e}}_{\text{downward}}}=W\sin \theta \] and frictional force as \[\dfrac{W}{20}\ and \sin \theta =\dfrac{1}{10}\].
Downhill Force \[=\text{ }\dfrac{W}{10}-\dfrac{W}{20}\]
\[=\dfrac{W}{20}\]
Hence, the power developed due to the force and velocity of driving is:
\[P=F\times v\]
Placing the values as found above and in the question, we get the power as:
\[P=\dfrac{W}{20}\times v\]
\[=\dfrac{W}{20}v\]
Now the power developed due to moving downward is \[\dfrac{P}{2}\]. Hence, equating both the power i.e. downhill and uphill, we get the velocity as:
\[\dfrac{{{P}_{up}}}{2}={{P}_{down}}\]
\[\Rightarrow \dfrac{3W}{4}=\dfrac{W}{20}v\]
\[\Rightarrow v=\dfrac{3W}{4}\times \dfrac{20}{W}\]
\[\Rightarrow v=15m/\sec \]
The velocity of the car when moving down is \[15m/\sec \].

Note:
Students may make mistake while calculating the power when the car is going downhill in downhill motion, the downward motion force will be subtracted from the frictional force which will be applied upward and after that we will equate both the powers remember both the powers will are same it is just that the downhill power is half that of the uphill force meaning the power of the downhill is not half but that of the uphill hence avoid halving off the downhill power and then equating it with the uphill. First equate both the power and then divide the result by half.