Question

A car of mass m is on an icy driveway inclined at an angle \[\theta \] as in the following Figure (a) Find the acceleration of the car, assuming the driveway is frictionless (b) Suppose the car is released from rest at the top of the distance from the car's bumper to the bottom of the incline is d. How long does it take the front bumper to reach the bottom of the hill, and what is the car's speed as it arrives there?

Answer 1

Hint: First form the components of the car’s force due to downward acceleration and due to the car's gravity. After that equate both the force and find the acceleration by eliminating the mass on both sides. After getting the acceleration of the car we find the velocity using the formula:
\[{{v}^{2}}={{u}^{2}}+2aS\]
And for the time taken to cover the inclined plane we use the formula:
\[S=ut+\dfrac{1}{2}a{{t}^{2}}\]
where S is the distance covered, u is the initial velocity, v is the final velocity, t is the time taken, a is the acceleration.

Complete step by step answer:
Drawing a block diagram of the question given above to show the components of force (both acceleration of the car and acceleration due to gravity) on an inclined plane of angle \[\theta \].

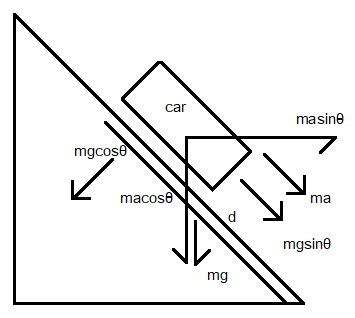
(a) Now let us solve for the first part where the driveway is assumed frictionless meaning the car slides down the inclined plane easily and to find the acceleration the we will equate the car’s force acceleration with car’s force acceleration due to gravity and if the force due to gravity is not in a same plane as that of the force due to car’s acceleration then we will equate the car’s acceleration force to one of the component of the force generated by the car due to gravity. Seeing the diagram we can say that both \[ma\] and \[mg\sin \theta \] are on the same plane. Therefore, if equating together the force will be:
Force of the car due to the car's motion down the inclined plane = Force of the car due to acceleration due to gravity.
\[ma=mg\sin \theta \]
\[\Rightarrow a=g\sin \theta \]
Therefore, the acceleration with which the car comes down is \[a=g\sin \theta \].
(b) Let us take the distance of the car on the inclined plane to the bottom of the inclined plane as \[d\].
From the first part we have the acceleration of the car in terms of gravity and sine component, now we will use that acceleration to find the velocity of the car moving down the inclined plane. The initial velocity of the car is zero as it is at rest on the top hence; we will calculate the final velocity placing the value in the formula to find the velocity as:
\[{{v}^{2}}={{u}^{2}}+2aS\]
\[\Rightarrow {{v}^{2}}=2\times g\sin \theta \times d\]
\[\Rightarrow v=\sqrt{2g\sin \theta d}\]
Thereby, the velocity with which it comes down the inclined plane is \[v=\sqrt{2g\sin \theta d}\].
Now for the time taken to climb down the inclined plane, we will use the displacement formula here we know the acceleration and velocity and displacement thereby placing the values in the formula, we get:
\[S=ut+\dfrac{1}{2}a{{t}^{2}}\]
With initial velocity as zero, and S as d and \[a=g\sin \theta \], we get the time taken as:
\[\Rightarrow d=\dfrac{1}{2}g\sin \theta {{t}^{2}}\]
\[\therefore t=\sqrt{\dfrac{2d}{g\sin \theta }}\]
Therefore, the time taken to cover the distance d on the inclined plane is \[t=\sqrt{\dfrac{2d}{g\sin \theta }}\].

Note:
Both the formula \[S=ut+\dfrac{1}{2}a{{t}^{2}}\] and \[v=u+at\] can be used to find the time taken to cover the distance d of the inclined plane. As we have all the other variables to find the unit of time. Hence, neither of the formulas are wrong.