Question

A car moving along a circular track of radius 50m accelerates from rest at $3m/{s^2}$. Consider a situation when the car's centripetal acceleration equals its tangential acceleration.
A. The angle around the track does the car travel is 1 rad.
B. The magnitude of the car’s total acceleration at that instant is$3\sqrt 2 m/{s^2}$.
C. Time elapsed before this situation is $\sqrt {\dfrac{{50}}{3}} \sec $
D. The distance travelled by the car during this time was 25m.

Answer 1

Hint: As given in question, centripetal acceleration becomes equal to the tangential acceleration is $3m/{s^2}$ then calculate total acceleration, time, distance and angle around the track of car using their basic mathematical expressions by substituting this value.
Formula used:
$\eqalign{
  & {v^2} - {u^2} = 2as \cr
  & \alpha = \dfrac{a}{R} \cr
  & \theta = {\omega _o}t + \alpha {t^2} \cr} $

Complete answer:
We know that the car is moving in circular motion such that the tangential acceleration and centripetal acceleration are equal. Mathematically this can be written as:
${a_T} = {a_C} = 3m/{s^2}$

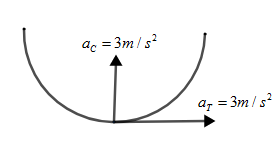
Firstly calculate the magnitude of total acceleration which will become equal to $\sqrt {{a_C}^2 + {a_T}^2} $
Total acceleration =
$\eqalign{
  & \sqrt {{{\left( 3 \right)}^2} + {{\left( 3 \right)}^2}} \cr
  & = \sqrt {9 + 9} \cr
  & = \sqrt {18} \cr} $
So, totals acceleration = $3\sqrt 2 m/{s^2}$
Now calculate time
$\dfrac{{{v^2}}}{r} = 3$
Consider where r represents the radius of track having a value of 50m.
$\eqalign{
  & \dfrac{{{v^2}}}{{50}} = 3 \cr
  & \Rightarrow {v^2} = 150 \cr
  & \therefore v = \sqrt {150} m/s \cr} $
We know that,
$\eqalign{
  & v = at \cr
  & \Rightarrow t = \dfrac{v}{a} \cr
  & \Rightarrow t = \dfrac{{\sqrt {150} }}{{\sqrt 9 }} \cr
  & \therefore t = \sqrt {\dfrac{{50}}{3}} \sec \cr} $
Now find the distance travelled by car.
$\eqalign{
  & {v^2} - {u^2} = 2as \cr
  & \Rightarrow 150 = 2\left( 3 \right)s \cr
  & \therefore s = \dfrac{{150}}{6} = 25m. \cr} $
To calculate the angle θ we need α angular acceleration (α) = $\dfrac{a}{R}$
$\alpha = \dfrac{3}{{50}}rad/{s^2}$
We know that,
$\eqalign{
  & \theta = {\omega _0}t + \alpha {t^2} \cr
  & \Rightarrow \theta = 0 + \dfrac{3}{{50}} \times \dfrac{{50}}{3} \cr
  & \therefore \theta = 1rad \cr} $

Therefore, all the given options A, B, C, and D are correct.

Additional Information:
If the velocity of a particle remains constant as time passes, we say that it is moving with a uniform velocity. If the velocity changes with time, it is said to be accelerated. So acceleration is the rate of change of velocity for a given system. Centripetal acceleration of a system is defined as the acceleration which is directed towards the center of the circle. Tangential acceleration, as the name suggests, acts at every point tangent to that point.

Note:
It should be remembered that to calculate the time, we need to find the velocity first. To calculate $\theta $ which is the angle around the track of car, we must calculate the angular acceleration that is α, whose units are $\dfrac{{rad}}{{{s^2}}}.$