Question

A car moves towards east with velocity 20 m/s then moves towards north with velocity 15 m/s. What will be the resultant velocity and direction?

Answer 1

Hint:Show the direction of velocity towards the east and towards the north in the diagram. It will form a right angle triangle. Then using Pythagoras theorem, you can determine the magnitude of resultant velocity. Using the property of trigonometry, express the angle between resultant velocity and velocity towards the east.

Complete step by step answer:
We have given that the car moves towards east with velocity \[{v_x} = 20\,{\text{m/s}}\] and then towards with velocity \[{v_y} = 15\,{\text{m/s}}\].

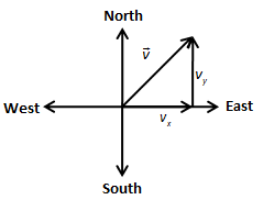
From the above figure, we can express the magnitude of resultant velocity \[v\] as,
\[v = \sqrt {v_x^2 + v_y^2} \]
Here, \[{v_y}\] is the velocity towards the north and \[{v_x}\] is the velocity towards the east.
Substituting \[{v_x} = 20\,{\text{m/s}}\] and \[{v_y} = 15\,{\text{m/s}}\] in the above equation, we get,
\[v = \sqrt {{{\left( {20} \right)}^2} + {{\left( {15} \right)}^2}} \]
\[ \Rightarrow v = \sqrt {400 + 225} \]
\[ \Rightarrow v = \sqrt {625} \]
\[ \Rightarrow v = 25\,{\text{m/s}}\]
Therefore, the resultant velocity of the particle is 25 m/s.

We can determine the direction of the resultant velocity using the simple trigonometry as follows,

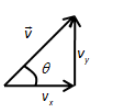
From the above figure, we can write,
\[\tan \theta = \dfrac{{{v_y}}}{{{v_x}}}\]
Here, \[{v_y}\] is the velocity towards the north and \[{v_x}\] is the velocity towards the east.
Substituting \[{v_x} = 20\,{\text{m/s}}\] and \[{v_y} = 15\,{\text{m/s}}\] in the above equation, we get,
\[\tan \theta = \dfrac{{15}}{{20}}\]
\[ \Rightarrow \tan \theta = 0.75\]
\[ \Rightarrow \theta = {\tan ^{ - 1}}\left( {0.75} \right)\]
\[ \therefore \theta = 37^\circ \]

Thus, the direction of resultant velocity is \[37^\circ \]towards the north with respect to east.

Note:One can also define the east direction as \[\hat i\] and the north direction as \[\hat j\]. Therefore, the direction of resultant velocity would be \[\vec v = {v_x}\hat i + {v_y}\hat j\]. The direction of velocity can be stated as \[37^\circ \] northeast. To determine the angle made by the resultant vector, the velocity is not necessarily converted into m/s since it is the ratio of two velocities.