Question

A capacitor of capacity$10\mu F$ is charged to $40$$V$ and a second capacitor of capacity $15\mu F$ is charged to $30$$V$. If the capacitors are connected in parallel, the amount of charge that flows from the smaller capacitor to higher capacitor in $\mu C$ is
A. $30$
B. $60$
C. $200$
D. $250$

Answer 1

Hint: When the charged capacitors are connected in parallel, the charge on the capacitors will be distributed in such a way that the potential across the capacitors will be the same. To get the charges appearing on each capacitor, think about how and where the charges are distributed.

Complete step by step answer:
First, we find the charge appeared on the capacitors when they were charged to some potential.For the capacitor of capacity $10\mu F$. The charge on the capacitor will be $Q = CV$, where $C$ is the capacitance of the capacitor and $V$ is the potential up to which the capacitor is charged.
$Q = \left( {10} \right)\left( {40} \right)$
$\Rightarrow Q = 400\mu F$.
Now, for the capacitor of capacity $15\mu F$,
$
Q = \left( {15} \right)\left( {30} \right) \\
\Rightarrow Q = 450\mu F \\
$
The figure shows the appeared charges before and after the connection.

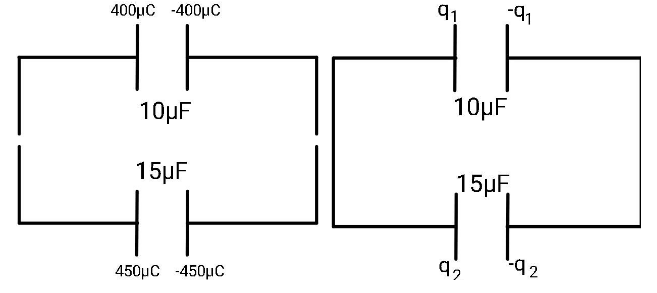
Think that how and where the charges are distributed? A particular amount of charge will flow from one of the capacitors to the other. The question is from which capacitor to which.
As they are connected in parallel, the potential difference across each capacitor will be equal. The potential across a capacitor is given as $V = \dfrac{Q}{C}$. Therefore,
$V = \dfrac{{{q_1}}}{{{C_1}}} = \dfrac{{{q_2}}}{{{C_2}}}$
$
\Rightarrow \dfrac{{{q_1}}}{{10}} = \dfrac{{{q_2}}}{{15}} \\
\Rightarrow {q_2} = \dfrac{{3{q_1}}}{2} \\
 $
As the charges are just rearranging/distributing, the net charge will be the same. Meaning that the charge is conserved.
$
{q_1} + {q_2} = 400 + 450 \\
\Rightarrow {q_1} + {q_2} = 850 \\
 $
Substituting the value of ${q_2}$ in the above equation,
\[
{q_1} + \dfrac{{3{q_1}}}{2} = 850 \\
\therefore {q_1} = 340\mu C \\
 \]
Therefore, the final charge on the \[10\mu F\] capacitor is $340\mu C$. As you can see, the initial charge at this capacitor was $400\mu C$ and now the charge is $340\mu C$. $60\mu C$ is flown out from the \[10\mu F\] capacitor. This $60\mu C$ charge will flow from \[10\mu F\] capacitor to $15\mu F$ capacitor.

Hence, the amount of charge that flows from the smaller capacitor to higher capacitor in $\mu C$ is $60$ and Option B is the correct answer.

Note: In this question, it is not specified which plate is connected to which, whether the positive plate of one capacitor is connected to the positive plate of the other or the positive plate of one capacitor is connected to the negative plate of the other. While solving the question, we assumed that the positive plates of each capacitor are connected together. If this was not the case, the answer would have come out to be different.