Question

A capacitor contains two square plates with side lengths 5.0 cm. The plates are separated by 2.0 mm. Dry air fills the space between the plates. Dry air has a dielectric constant of 1.00 and experiences dielectric breakdown when the electric field exceeds $3.0 \times {10^4}$ V/cm.
What is the magnitude of the charge that can be stored on each plate before the capacitor exceeds its breakdown limit and sends a spark between the plates?
A) $6.6 \times {10^{ - 8}}C$
B) $6.6 \times {10^{ - 5}}C$
C) $3.3 \times {10^{ - 7}}C$
D) $3.3 \times {10^{ - 84}}C$
E) $8.1 \times {10^{ - 2}}C$

Answer 1

Hint: We can calculate the area of the square plates as the length of its side is given (area of a square is equal to the square of its side). This can be used to calculate the value of capacitance of the capacitor which in turn would help to calculate the required value of charge.

Formula Used:
1. Capacitance of a parallel plate capacitor:
$C = \dfrac{{A{\varepsilon _0}}}{d}$ where,
C = Capacitance
A = Area of plates
d = Distance of between the plates
2. Potential difference of a parallel plate capacitor:
V = Ed where,
E = Electric field
V = Potential difference
3. Capacitance:
$C = \dfrac{Q}{V}$ where,
Q = Charge

Complete step by step answer:

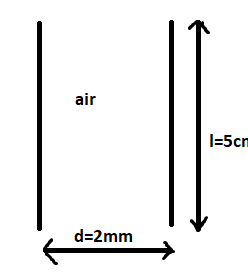
Given:
Length of plate (l) = 5.0 cm
                                  = $\dfrac{5}{{100}}$ m or 0.05 m
Distance between the plates (d) = 2.0 mm
                                                          = $\dfrac{2}{{1000}}$ m or 0.002 m
Electric field $\left( {\overrightarrow E } \right)$ = $3.0 \times {10^4}$ V/cm.
                                = $3.0 \times {10^6}$ V/m.
Now,
As the plates are square in shape their area is given as:
A = ${l^2}$
Substituting the value:
A = ${(0.05m)^2}$or ${\left( {5 \times {{10}^{ - 2}}} \right)^2}$
 A = $25 \times {10^{ - 4}}{m^2}$ _____ (1)
Capacitance and potential difference of a parallel plate capacitor is given as:
$C = \dfrac{{A{\varepsilon _0}}}{d}$
V = Ed
Capacitance is defined as charge per unit potential difference:
$C = \dfrac{Q}{V}$
The value of charge in terms of capacitance and voltage is:
Q = CV
Substituting these values:
$Q = \dfrac{{A{\varepsilon _0}}}{d} \times Ed$
Q = $A{\varepsilon _0}E$ here,
A = $25 \times {10^{ - 4}}{m^2}$
${\varepsilon _0} = 8.85 \times {10^{ - 12}}$
Substituting these values, we get:
Q = $25 \times {10^{ - 4}} \times 8.85 \times {10^{ - 12}} \times 3.0 \times {10^6}$
Q = $6.6 \times {10^{ - 8}}$
The SI units of charge is coulombs (C)
Q = $6.6 \times {10^{ - 8}}$C
Therefore, the magnitude of the charge that can be stored on each plate before the capacitor exceeds its breakdown limit and sends a spark between the plates is $6.6 \times {10^{ - 8}}$C.

Note:The dielectric constant here was 1 and thus neglected but in general it can be defined as the ratio of permittivity of a substance with that of vacuum.
For the conversions remember: 1 m is equal to 100 cm and is also equal to 1 mm
The dry air mentioned in the question is nothing but the air with less humidity.