Question

A cable of a suspension bridge is in the form of a parabola whose span is 40m. The road way is 5m below the lowest point of the cable. An extra support is provided across the cable 30m above the ground level. Find the length of the support if the heights of the pillars are 55m.

Answer 1

Hint: A parabola is a plane curve which is mirror-symmetrical and is approximately U-shaped. It is a curve where any point is at an equal distance from a fixed point (the focus) and a fixed straight line (the directrix).
The focus of a parabola is a fixed point on the interior and the directrix is perpendicular to the axis of symmetry of a parabola and does not touch the parabola.
Here, we use the equation of parabola${x^2} = 4ay$, as the parabola is symmetric to the y-axis.
With the help of the information given in the question, we find the coordinate of the point A. We will find the value of ‘a’ by putting the value of coordinates in the equation of parabola. And as we know the y-coordinate of the support, so we can easily find out the length of the support with the equation of parabola.

Complete step-by-step answer:
Using the equation, ${x^2} = 4ay$
According to the question,

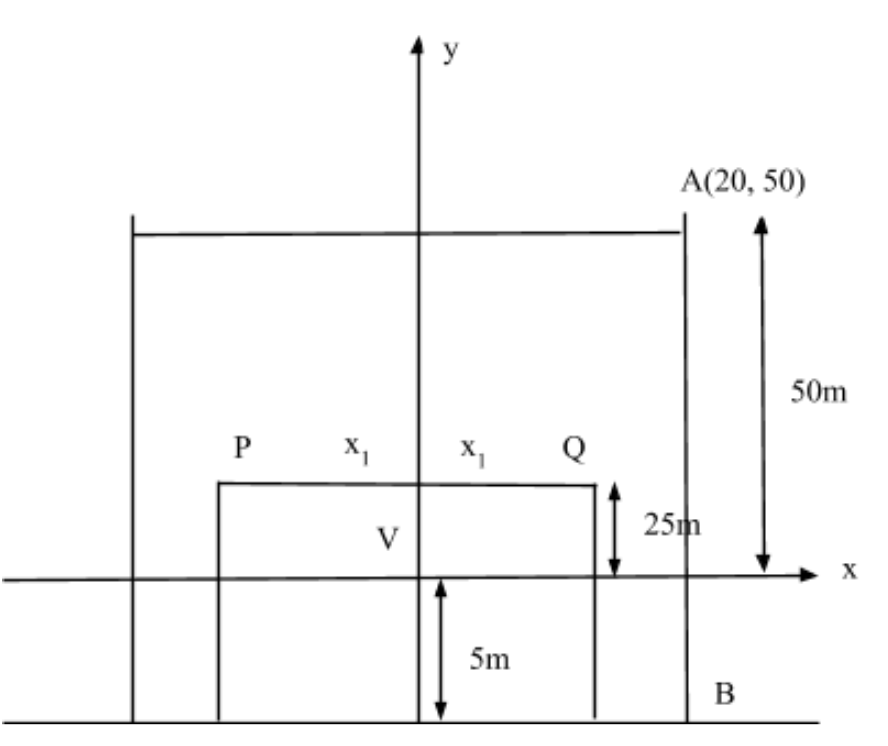
Since, the span of the parabola is 40m.
So, x-coordinate of A = 20 (half of span of the parabola)
The heights of the pillars = AB = 55m
So, the coordinates of point A = (20, 50)
So, put x=20 and y=50 in ${x^2} = 4ay$
$\begin{gathered}
  {\left( {20} \right)^2} = 4 \times a \times 50 \\
  400 = 4a \times 50 \\
  400 = 200a \\
\end{gathered} $
$\begin{gathered}
  a = \dfrac{{400}}{{200}} \\
  a = 2 \\
\end{gathered} $
Let the support be PQ
So, the equation of the parabola gets reduced to
${x^2} = 8y$
Identifying the point Q$\left( {{x_1},25} \right)$
$\begin{gathered}
  {x_1} = 10\sqrt 2 \\
  PQ = 2{x_1} = 2 \times 10\sqrt 2 \\
  PQ = 20\sqrt 2 \\
\end{gathered} $

Note: One important feature of the parabola is that it has an extreme point, called the vertex. If the parabola opens up, the vertex represents the lowest point on the graph, or the minimum value of the quadratic equation. If the parabola opens down, the vertex represents the highest point on the graph, or the maximum value.