Question

A bullet of mass m moving with velocity v strikes a suspended wooden block of mass M.1f the block rises to height h, then the initial velocity v the bullet must have been:
A) $\sqrt{\text{2gh}}$
B) $\dfrac{\text{M+m}}{\text{2m}}\sqrt{\text{2gh}}$
C) $\dfrac{\text{m}}{\text{M+m}}\sqrt{\text{2gh}}$
D) $\dfrac{\text{M+m}}{\text{m}}\sqrt{\text{2gh}}$

Answer 1

Hint: The law of momentum conservation is considered to be one of the most powerful laws in physics. The law of momentum conservation can be stated as, for collision operating between object 1 and object 2, in an isolated system, the total momentum of the two objects before the collision is equivalent to the total momentum of the two objects after their collision. That is, the moments lost in object 1 is equal to the moments gained by object 2. Keeping this law of momentum conservation in mind, we can solve any questions like this.

Complete step by step answer:
Using the conservation of momentum, we can solve this question. Let us consider a variable V, which is the velocity combined after the bullet hits the block. The diagram is shown below:

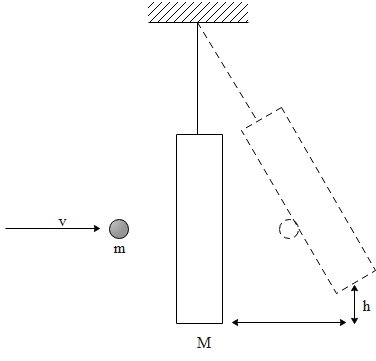
$\text{mv = (m+M)V (i)}$
When the block rises up in height, the kinetic energy of the block gets converted into potential energy. Taking these cases into consideration, we get,
$\begin{align}
  & \dfrac{\text{1}}{\text{2}}\left( \text{m+M} \right){{\text{V}}^{\text{2}}}\text{ = }\left( \text{m+M} \right)\text{gh} \\
 & \Rightarrow \text{ }{{\text{V}}^{\text{2}}}\text{ = 2gh} \\
 & \Rightarrow \text{ V = }\sqrt{\text{2gh}}\text{ }\ldots \text{(ii)} \\
\end{align}$
From the given equations, we can combine equations (i) and (ii) to derive the following equation:
$\begin{align}
  & \text{mv = (m+M) }\!\!\times\!\!\text{ }\sqrt{\text{2gh}} \\
 & \Rightarrow \text{ v = }\dfrac{\text{(m+M) }\!\!\times\!\!\text{ }\sqrt{\text{2gh}}}{\text{m}}\text{ } \\
\end{align}$
Hence, the correct answer is $\dfrac{M+m}{m}\sqrt{2gh}$.
Therefore, the correct option is Option D.

Note: We should know that in practical situations, a little amount of mass always turns energy (or a little energy turns into mass). But the addition of mass and energy is always conserved. To create energy we have to destroy the appropriate amount of mass. This concept is explained in the formula E = m$c^2$.