Question

A bullet is to be fired with a speed of 2000 m/s to hit the target of 200 m away on a level ground. If g = 10 m/$s^2$, then the gun should be aimed at
$\left( A \right)$ Directly at the target
$\left( B \right)$ 5 cm below the target
$\left( C \right)$ 5 cm above the target
$\left( D \right)$ 2 cm above the target

Answer 1

- Hint: In this question use the concept that if we directly hit the target due to Earth’s gravity it will not hit the target i.e. it is hit below the target so we have to aim the bullet above the target so that it hit the desired target so use projectile motion concept to reach the solution of the question.

Formula used – $R = \dfrac{{{u^2}\sin 2\theta }}{g}$

Complete step-by-step solution -

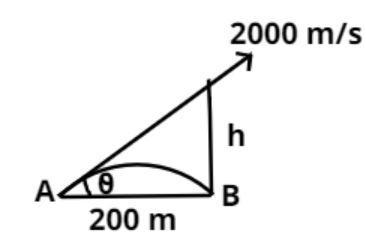
As we know that the Earth’s gravity is acting downwards on the bullet so if we fired the bullet directly at the target the bullet did not hit the target due to gravity it hits below the target.
So we have to aim the gum at an angle $\theta $ so that it follows a parabolic path just like the projectile motion to hit the desired target as shown in the above figure.
So we have to calculate the h (at which the gun is aimed)
So according to Projectile motion the range R is given as
$ \Rightarrow R = \dfrac{{{u^2}\sin 2\theta }}{g}$, where R = 200 m, u = initial velocity = 2000 m/s and g = Earth’s gravity = 10 m/$s^2$.
$ \Rightarrow 200 = \dfrac{{{{\left( {2000} \right)}^2}\sin 2\theta }}{{10}}$
$ \Rightarrow \sin 2\theta = \dfrac{1}{{2000}}$
Now as we see that $\theta $ is small so, $\sin 2\theta \simeq 2\theta $
$ \Rightarrow 2\theta = \dfrac{1}{{2000}}$
$ \Rightarrow \theta = \dfrac{1}{{4000}}$................. (1)
Now as we know that tan is the ratio of perpendicular to base therefore, from figure
$ \Rightarrow \tan \theta = \dfrac{h}{{200}}$
Now as we see that $\theta $ is small so, $\tan \theta \simeq \theta $
$ \Rightarrow \theta = \dfrac{h}{{200}}$
Now from equation (1) we have,
$ \Rightarrow \dfrac{1}{{4000}} = \dfrac{h}{{200}}$
$ \Rightarrow h = \dfrac{{200}}{{4000}} = \dfrac{1}{{20}}$meter
Now as we know that 1 m = 100 cm
So (1/20) m = (100/20) = 5 cm.
Therefore, h = 5 cm
So we have to aim the gun 5 cm above the target.
So this is the required answer.

Hence option (C) is the correct answer.

Note: Whenever we face such types of questions always remember we have to aim the gun above the target so that it makes a parabolic path to hit the target so use projectile motion range formula which is stated above and calculate the angle by which we have to aim the gun above the ground than use the tan formula as above and calculate the height by which we have to aim the gun above the target.