A bullet fired horizontally with a speed of $400m/\sec $. It strikes a wooden block of mass $5kg$ initially at rest placed on a horizontal floor as shown in the figure. It emerges with a speed of $200m/\sec $ and the block slides a distance of $20cm$ before coming to rest. If the coefficient of friction between the block and the surface is $\dfrac{\lambda }{50}$, then find $\lambda $. Mass of the bullet is $20gm$ (take$g=10m/{{s}^{2}}$).
Answer
Verified584.1k+ views
Hint: This problem can be solved by finding out the velocity of the block after the bullet comes out from it using the principle of conservation of momentum. Then, the deceleration of the block due to the frictional force on the block can be calculated by using the equations of motion for constant acceleration. This can then be compared by the acceleration due to frictional force using the relation $\dfrac{\lambda }{50}$ given in the question.
Formula used:
When no external force acts on a system, the total momentum of the system is conserved. Hence,
$\sum{{{M}_{i}}{{v}_{i}}=\sum{{{M}_{f}}{{v}_{f}}}}$
Where ${{M}_{i}}$ and ${{M}_{f}}$ are the total masses of the initial and final state of the system and ${{v}_{i}}$ and ${{v}_{f}}$ are the velocities of the masses in the initial and final state of the system.
${{F}_{friction}}=\mu N$
where ${{F}_{friction}}$ is the force of friction on a body by a surface, $N$is the normal force on the surface by the body, $\mu $is the coefficient of friction of the surface.
$F=ma$
where $F$ is the force exerted on or by a body, $m$is the mass of the body and $a$ is the acceleration of that body due to that force.
For uniform motion with constant acceleration,
$\dfrac{{{v}^{2}}-{{u}^{2}}}{2s}=a$ --(Equation of motion for constant acceleration)
where $v$ ,$u$ are the final and initial velocities of the body, $s$is the displacement covered by the body.
Complete step by step answer:
First we will use the principle of conservation of momentum to find out the velocity of the block. Then we will use the equations for uniform motion with constant acceleration, to find out the deceleration of the block due to the frictional force and then compare this to the general deceleration offered by a frictional force. In this way, we can find out the required value of the coefficient of friction of the surface.
Therefore let us analyze the question.
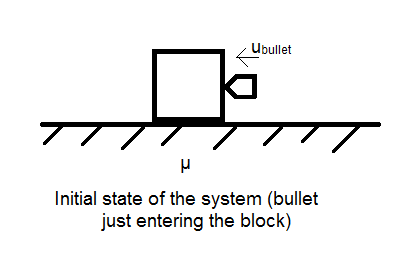
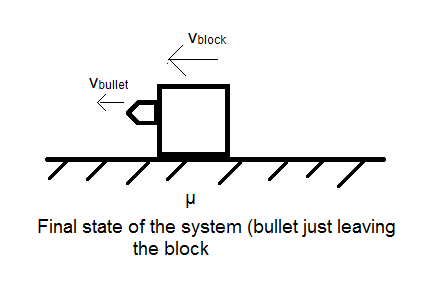
We will consider the bullet and the block as a single system. Now, since there are no external forces on the system and only the block applies a force on the bullet and vice versa, that is there are only internal forces on the system, the total momentum of the system shall be conserved.
The principle of conservation of momentum states that when no external forces act on the system, the total momentum of the system is conserved. That is,
$\sum{{{M}_{i}}{{v}_{i}}=\sum{{{M}_{f}}{{v}_{f}}}}$
Where ${{M}_{i}}$ and ${{M}_{f}}$ are the total masses of the initial and final state of the system and ${{v}_{i}}$ and ${{v}_{f}}$ are the velocities of the masses in the initial and final state of the system.
Now, let the mass of the block and the bullet be $M$ and $m$, respectively.
Therefore given,
$M=5kg$
$m=20gm=0.02kg$ $\left( \because 1gm=0.001kg \right)$
We will consider the initial state of the system to be at the moment just before the bullet enters the block and the final state to be the moment just after the bullet leaves the block.
Hence, initial velocity of the bullet ${{u}_{bullet}}=400m/s$
Initial velocity of the block ${{u}_{block}}=0$(since the block was at rest)
Final velocity of the bullet ${{v}_{bullet}}=200m/s$
final velocity of the block is ${{v}_{block}}$.
Hence, applying the principle of conservation of momentum,
$M{{u}_{block}}+m{{u}_{bullet}}=M{{v}_{block}}+m{{v}_{bullet}}$
$\therefore \left( 5\times 0 \right)+\left( 0.02\times 400 \right)=\left( 5\times {{v}_{block}} \right)+\left( 0.02\times 200 \right)$
$\therefore 0+8=5{{v}_{block}}+4$
$\therefore 8-4=5{{v}_{block}}$
$\therefore 4=5{{v}_{block}}$
$\therefore {{v}_{block}}=\dfrac{4}{5}=0.8m/\sec $ ---(1)
Therefore, the block starts moving on the rough surface with a velocity of $0.8m/\sec $
Now, we will try to find out the frictional force on the block.
${{F}_{friction}}=\mu N$ ---(2)
where ${{F}_{friction}}$is the force of friction on a body by a surface, $N$ is the normal force on the surface by the body, $\mu $ is the coefficient of friction of the surface.
Now, since the block does not move in the vertical axis, the sum of all vertical forces on it must be zero (which is a condition for equilibrium).
The vertical forces on the block are the upward normal force on the block by the surface and the downward force of gravity, that is, its own weight. For equilibrium, these two must balance each other in magnitude.
Hence,
$\text{Normal force on the block by the surface = Weight of the block}$
$\therefore N=Mg$
Where $N$is the normal force on the block by the surface, $M$is the mass of the block and $g$is the acceleration due to gravity equal to $10m/{{\sec }^{2}}$.
Hence, plugging in the values, we get,
$N=5\times 10=50Newton$
Hence, the normal force on the block is $50N$--(3).
Therefore, putting (3) in (2), we get,
${{F}_{friction}}=\mu \times 50$
Now, as given in the question, $\mu =\dfrac{\lambda }{50}$. Hence, plugging in this value in the above equation, we get,
${{F}_{friction}}=\dfrac{\lambda }{50}\times 50=\lambda $ --(4)
Hence, the frictional force exerted by the surface on the block is $\lambda Newton$.
Now,
$F=ma$
where $F$ is the force exerted on or by a body, $m$is the mass of the body and $a$ is the acceleration of that body due to that force.
Therefore, using this, the acceleration produced by the surface on the block is
$a=\dfrac{{{F}_{friction}}}{M}=-\dfrac{\lambda }{5}$
The negative sign comes because the frictional force is trying to oppose the motion of the block and hence is decelerating it.
Now, for uniform motion with constant acceleration,
$\dfrac{{{v}^{2}}-{{u}^{2}}}{2s}=a$ --(Equation of motion for constant acceleration) --(5)
where $v$ ,$u$ are the final and initial velocities of the body, $s$is the displacement covered by the body.
Now, let the initial velocity of the block in this case is ${{v}_{block}}=0.8m/\sec $
The final velocity of the block is $0m/\sec $, since it comes to rest.
The acceleration of the block is $-\dfrac{\lambda }{5}$
And the displacement covered by it is $20cm=0.2m$ $\left( \because 1cm=0.01m \right)$
Plugging these values in equation (5), we get,
$\dfrac{{{0}^{2}}-{{0.8}^{2}}}{2\times 0.2}=-\dfrac{\lambda }{50}$
$\therefore \dfrac{-0.64}{0.4}=\dfrac{-\lambda }{5}$
$\therefore 1.6=\dfrac{\lambda }{5}$
$\therefore \lambda =1.6\times 5=8$
Hence, the value of $\lambda $ is 8.
Note: Block and bullet type of problems are very common in the topic of conservation of momentum. One must be careful that the principle of conservation of momentum is only applicable when there are no external forces on the system. Thus, one must learn to choose the system properly. Doing so, allows us to apply this principle which is very useful in such problems.
A general point to be noted is that when writing the velocities for the bodies in a system during conservation of momentum, the proper directions of the velocities should also be considered and not only the magnitudes of the velocities. If two velocities are in opposite directions, then their respective momenta should be subtracted and not added. In this problem the final velocities of both the bodies were in the same direction, so their momenta were added. However, if they were in opposite directions, they would have to be subtracted.
Formula used:
When no external force acts on a system, the total momentum of the system is conserved. Hence,
$\sum{{{M}_{i}}{{v}_{i}}=\sum{{{M}_{f}}{{v}_{f}}}}$
Where ${{M}_{i}}$ and ${{M}_{f}}$ are the total masses of the initial and final state of the system and ${{v}_{i}}$ and ${{v}_{f}}$ are the velocities of the masses in the initial and final state of the system.
${{F}_{friction}}=\mu N$
where ${{F}_{friction}}$ is the force of friction on a body by a surface, $N$is the normal force on the surface by the body, $\mu $is the coefficient of friction of the surface.
$F=ma$
where $F$ is the force exerted on or by a body, $m$is the mass of the body and $a$ is the acceleration of that body due to that force.
For uniform motion with constant acceleration,
$\dfrac{{{v}^{2}}-{{u}^{2}}}{2s}=a$ --(Equation of motion for constant acceleration)
where $v$ ,$u$ are the final and initial velocities of the body, $s$is the displacement covered by the body.
Complete step by step answer:
First we will use the principle of conservation of momentum to find out the velocity of the block. Then we will use the equations for uniform motion with constant acceleration, to find out the deceleration of the block due to the frictional force and then compare this to the general deceleration offered by a frictional force. In this way, we can find out the required value of the coefficient of friction of the surface.
Therefore let us analyze the question.
We will consider the bullet and the block as a single system. Now, since there are no external forces on the system and only the block applies a force on the bullet and vice versa, that is there are only internal forces on the system, the total momentum of the system shall be conserved.
The principle of conservation of momentum states that when no external forces act on the system, the total momentum of the system is conserved. That is,
$\sum{{{M}_{i}}{{v}_{i}}=\sum{{{M}_{f}}{{v}_{f}}}}$
Where ${{M}_{i}}$ and ${{M}_{f}}$ are the total masses of the initial and final state of the system and ${{v}_{i}}$ and ${{v}_{f}}$ are the velocities of the masses in the initial and final state of the system.
Now, let the mass of the block and the bullet be $M$ and $m$, respectively.
Therefore given,
$M=5kg$
$m=20gm=0.02kg$ $\left( \because 1gm=0.001kg \right)$
We will consider the initial state of the system to be at the moment just before the bullet enters the block and the final state to be the moment just after the bullet leaves the block.
Hence, initial velocity of the bullet ${{u}_{bullet}}=400m/s$
Initial velocity of the block ${{u}_{block}}=0$(since the block was at rest)
Final velocity of the bullet ${{v}_{bullet}}=200m/s$
final velocity of the block is ${{v}_{block}}$.
Hence, applying the principle of conservation of momentum,
$M{{u}_{block}}+m{{u}_{bullet}}=M{{v}_{block}}+m{{v}_{bullet}}$
$\therefore \left( 5\times 0 \right)+\left( 0.02\times 400 \right)=\left( 5\times {{v}_{block}} \right)+\left( 0.02\times 200 \right)$
$\therefore 0+8=5{{v}_{block}}+4$
$\therefore 8-4=5{{v}_{block}}$
$\therefore 4=5{{v}_{block}}$
$\therefore {{v}_{block}}=\dfrac{4}{5}=0.8m/\sec $ ---(1)
Therefore, the block starts moving on the rough surface with a velocity of $0.8m/\sec $
Now, we will try to find out the frictional force on the block.
${{F}_{friction}}=\mu N$ ---(2)
where ${{F}_{friction}}$is the force of friction on a body by a surface, $N$ is the normal force on the surface by the body, $\mu $ is the coefficient of friction of the surface.
Now, since the block does not move in the vertical axis, the sum of all vertical forces on it must be zero (which is a condition for equilibrium).
The vertical forces on the block are the upward normal force on the block by the surface and the downward force of gravity, that is, its own weight. For equilibrium, these two must balance each other in magnitude.
Hence,
$\text{Normal force on the block by the surface = Weight of the block}$
$\therefore N=Mg$
Where $N$is the normal force on the block by the surface, $M$is the mass of the block and $g$is the acceleration due to gravity equal to $10m/{{\sec }^{2}}$.
Hence, plugging in the values, we get,
$N=5\times 10=50Newton$
Hence, the normal force on the block is $50N$--(3).
Therefore, putting (3) in (2), we get,
${{F}_{friction}}=\mu \times 50$
Now, as given in the question, $\mu =\dfrac{\lambda }{50}$. Hence, plugging in this value in the above equation, we get,
${{F}_{friction}}=\dfrac{\lambda }{50}\times 50=\lambda $ --(4)
Hence, the frictional force exerted by the surface on the block is $\lambda Newton$.
Now,
$F=ma$
where $F$ is the force exerted on or by a body, $m$is the mass of the body and $a$ is the acceleration of that body due to that force.
Therefore, using this, the acceleration produced by the surface on the block is
$a=\dfrac{{{F}_{friction}}}{M}=-\dfrac{\lambda }{5}$
The negative sign comes because the frictional force is trying to oppose the motion of the block and hence is decelerating it.
Now, for uniform motion with constant acceleration,
$\dfrac{{{v}^{2}}-{{u}^{2}}}{2s}=a$ --(Equation of motion for constant acceleration) --(5)
where $v$ ,$u$ are the final and initial velocities of the body, $s$is the displacement covered by the body.
Now, let the initial velocity of the block in this case is ${{v}_{block}}=0.8m/\sec $
The final velocity of the block is $0m/\sec $, since it comes to rest.
The acceleration of the block is $-\dfrac{\lambda }{5}$
And the displacement covered by it is $20cm=0.2m$ $\left( \because 1cm=0.01m \right)$
Plugging these values in equation (5), we get,
$\dfrac{{{0}^{2}}-{{0.8}^{2}}}{2\times 0.2}=-\dfrac{\lambda }{50}$
$\therefore \dfrac{-0.64}{0.4}=\dfrac{-\lambda }{5}$
$\therefore 1.6=\dfrac{\lambda }{5}$
$\therefore \lambda =1.6\times 5=8$
Hence, the value of $\lambda $ is 8.
Note: Block and bullet type of problems are very common in the topic of conservation of momentum. One must be careful that the principle of conservation of momentum is only applicable when there are no external forces on the system. Thus, one must learn to choose the system properly. Doing so, allows us to apply this principle which is very useful in such problems.
A general point to be noted is that when writing the velocities for the bodies in a system during conservation of momentum, the proper directions of the velocities should also be considered and not only the magnitudes of the velocities. If two velocities are in opposite directions, then their respective momenta should be subtracted and not added. In this problem the final velocities of both the bodies were in the same direction, so their momenta were added. However, if they were in opposite directions, they would have to be subtracted.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success
Master Class 12 Economics: Engaging Questions & Answers for Success
Master Class 12 English: Engaging Questions & Answers for Success
Master Class 12 Maths: Engaging Questions & Answers for Success
Master Class 12 Social Science: Engaging Questions & Answers for Success
Master Class 12 Chemistry: Engaging Questions & Answers for Success
Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE
Which animal has three hearts class 11 biology CBSE
10 examples of friction in our daily life
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE
1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE
Difference Between Prokaryotic Cells and Eukaryotic Cells