Question

A building is made by keeping the lower window of a building at a height of 2 m above the ground and its upper window 6 m vertically above the lower window in view to have proper sunlight. At a certain instant, the angle elevation of a balloon from these windows are observed to be 60° and 30° respectively. Find the height of the balloon above the ground. What values are depicted, if the building owner is in a view to use the proper sunlight by maintaining the level of height of the window in the building?

Answer 1

Hint: In this question using the given information and construct the diagram and make the right angled triangle and use the trigonometric identities for the right angled triangle, use this information to approach towards the solution of the question.

Complete step-by-step answer:
According to the given information we know that a building having two windows where lower windows are at 2 meter above the ground and upper window is vertically above 6 meter from lower window and there is a balloon outside the building at which angle of elevation from lower window is 30° and 60° from upper window
Now using the given information to construct the required structure

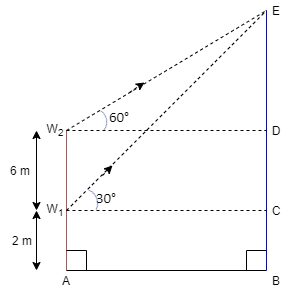
As we know that angle of elevation from upper window is 60°
So since we know that in a right angle triangle $\tan \theta = \dfrac{{perpendicular}}{{base}}$
Therefore in the triangle W₂DE
$\tan {60^ \circ } = \dfrac{{ED}}{{{W_2}D}}$
Since we know that $\tan {60^ \circ } = \sqrt 3 $
Substituting the values in the above equation
$\sqrt 3 = \dfrac{{ED}}{{{W_2}D}}$
$ \Rightarrow $$ED = \sqrt 3 {W_2}D$
Since for lower window the angle of elevation is 30° therefore for triangle W₁CE
$\tan {30^ \circ } = \dfrac{{EC}}{{{W_2}C}}$
Since we know that $\tan {30^ \circ } = \dfrac{1}{{\sqrt 3 }}$and by the above diagram we can say that EC = ED + DC
Substituting the values in the above equation we get
$\dfrac{1}{{\sqrt 3 }} = \dfrac{{ED + DC}}{{{W_2}C}}$
$ \Rightarrow $${W_2}C = \sqrt 3 \left( {ED + DC} \right)$
Substituting the value of ED in the above equation
${W_2}C = \sqrt 3 \left( {\sqrt 3 {W_2}D + 6} \right)$
$ \Rightarrow $${W_2}C = 3{W_2}D + 6\sqrt 3 $
Since we know that W₂C is equal to W₂D
Therefore ${W_2}C = 3{W_2}C + 6\sqrt 3 $
$ \Rightarrow $${W_2}C = 3{W_2}C + 6\sqrt 3 $
$ \Rightarrow $${W_2}C = 3\sqrt 3 $
$ \Rightarrow $${W_2}C = 3\sqrt 3 = {W_2}D$
Therefore $ED = \sqrt 3 \left( {3\sqrt 3 } \right)$
$ \Rightarrow $$ED = 9$ m
So the height of balloon from ground is equal to EB = ED + DB = 9 + 8 = 17 m
Therefore the balloon is 17 meter above ground with respect to the ground.

Note: The trigonometric identities we used in the above condition are only applicable for right angle triangles so in this case when a triangle have acute angle then the trigonometric functions shows the ratio of the 2 sides such as function of sin theta shows ratio of perpendicular and hypotenuse, cos theta shows the ratio of base and hypotenuse of the right angle triangle.