Question

A bucket tied at the end of the $ 1.6m $ long string is whirled in a vertical circle with constant speed. What should be the minimum speed so that the coater from the bucket does not spill when the buckets at the highest position? ( $ g = 10m{s^{ - 1}} $ )
(A) $ 16m{s^{ - 1}} $
(B) $ 6.25m{s^{ - 1}} $
(C) $ 4m{s^{ - 1}} $
(D) $ 2m{s^{ - 1}} $

Answer 1

Hint : Here, in the question it is clearly said that the bucket is tied to the string and whirled in vertical circle i.e. this is the concept of vertical circular motion. We must have a better understanding of the vertical circular motion and accordingly we can obtain the minimum velocity of the bucket where the coat could not be spilled.

Complete Step By Step Answer:
Let the radius of the vertical circle in which the bucket is whirled is the length of the string be $ R = 1.6m $ , velocity of the bucket be $ v $ and it is constant, $ m $ be the mass of the bucket, $ g $ is the acceleration due to gravity, $ N $ be the normal acting on the body along the radius of the circle.
Let us describe all these terms in the figure below:

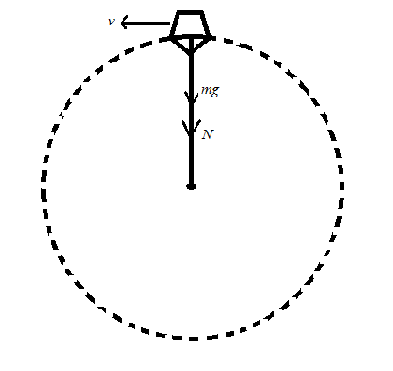
In the above figure we have the bucket tied to the string and whirling around in the vertical circle such that it has the constant velocity.
Now, let us equate the forces acting on the bucket along the radius of the circle.
 $ N + mg = {F_C} $ …( the centripetal force $ {F_C} $ is also acting along the radius )
 $ {F_C} = \dfrac{{m{v^2}}}{R} $
Therefore, the above equation becomes as:
 $ \Rightarrow N + mg = \dfrac{{m{v^2}}}{R} $
 $ \Rightarrow N = \dfrac{{m{v^2}}}{R} - mg $
But, $ N \geqslant 0 $ since, we do not want to spill the coat from the bucket
Thus, we have,
 $ \Rightarrow \dfrac{{m{v^2}}}{R} - mg \geqslant 0 $
 $ \Rightarrow v \geqslant \sqrt {gR} $
Now, minimum velocity at the top of the vertical circle is given by:
 $ {v_{\min }} = \sqrt {gR} = \sqrt {10 \times 1.6} m{s^{ - 1}} $
 $ \therefore {v_{\min }} = \sqrt {16} m{s^{ - 1}} = 4m{s^{ - 1}} $
Thus, the minimum required velocity at the top of the circle is $ 4m{s^{ - 1}} $
Hence, the correct answer is option C.

Note :
It’s been given in the question that the bucket is in a vertical circle, so it was necessary to use the vertical circular motion concept. As we know that in vertical motion we have to maintain the minimum speed so that we could not spill the coat from the bucket. We have calculated that speed with the help of equating forces acting on a bucket of vertical circle concepts.