Question

A bucket of height 8cm made up of copper sheet is in the form of frustum of a right circular cone with radii of lower and upper ends as 3cm and 9cm respectively. Calculate the height of the right circular cone.

Answer 1

Hint- In order to find the solution, we will first make the diagram with the help of given data then use the property as if a line cuts the two parallel lines then the corresponding angles made by the cutting line must be equal.

Complete step-by-step answer:

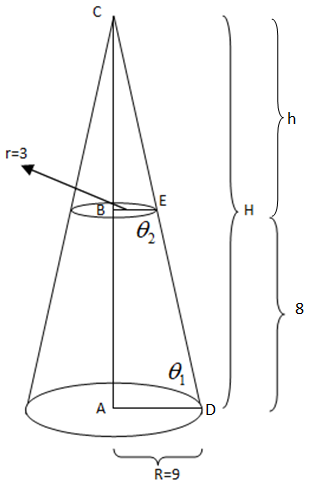
Given that
Height of bucket =8cm
Lower radius of bucket =3cm
Upper radius of bucket =9cm
In diagram H is the height of the right circular cone and AD and BE are the upper and lower radii respectively.
Take triangle $\Delta ABC$
$\tan {\theta _1} = \dfrac{{AC}}{{AD}}$
Put the value of AD as 9cm, we have
$\tan {\theta _1} = \dfrac{{AC}}{9}..............(1)$
Now, consider $\Delta BEC$
$\tan {\theta _2} = \dfrac{{BC}}{{BE}}$
Put the value of BE as 3cm, we have
$\tan {\theta _2} = \dfrac{{BC}}{3}$
As we know that, if a line cuts two parallel line then the corresponding angles made by the cutting lines are equal
$\therefore \tan {\theta _1} = \tan {\theta _2}$
By substituting the values of $\tan {\theta _1}\& \tan {\theta _2}$ form equation (1) and (2), we get

$
   \Rightarrow \dfrac{{AC}}{9} = \dfrac{{BC}}{3} \\
   \Rightarrow 3AC = 9BC \\
   \Rightarrow 3(8 + h) = 9h{\text{ }}\left[ {\because AC = 8 + h{\text{ and }}BC = h} \right] \\
   \Rightarrow 24 + 3h = 9h \\
   \Rightarrow 24 = 6h \\
   \Rightarrow h = 4{\text{cm}}{\text{.}} \\
$
Hence, the height of right circular cone $ = h + 8 = 4 + 8 = 12{\text{cm}}{\text{.}}$

Note- In order to solve these types of questions, it is important to draw diagrams first. This will help in understanding the problem and solving it. Also remember properties of angle such as corresponding angles, alternate angles and vertical angles. This will help in solving the questions and try to solve the problem in steps.