Question

A bucket is raised from a well by means of a rope which is wound around a wheel of diameter 77 cm. Given that the bucket ascends in 1 minute 28 seconds with a uniform speed of 1.1 m/sec, calculate the number of complete revolutions the wheel makes in raising the bucket.

Answer 1

Hint: Distance covered by the bucket using given time and speed can be calculated, distance covered by the bucket using circumference and revolutions can be calculated. Both of these speeds will be equal as they are for the ascending of the bucket.
Formulas to be used:
Circumference of a circle = $ 2\pi r $
\[speed = \dfrac{{dis\tan ce}}{{time}}\]
For conversions, remember:
1 min = 60 seconds
1 m = 100 cm or 100 cm = 1 m

Complete step-by-step answer:

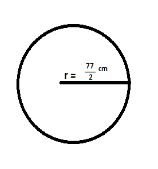
Given:
Diameter of wheel (d) = 77 cm
Time of bucket ascends in (t) = 1 minute 28 seconds
Speed of bucket ascending = Distance = m/s
Now,
Radius = Half the diameter.
 $
\Rightarrow r = \dfrac{d}{2} \
\Rightarrow r = \dfrac{{77}}{2}cm \
  $ [As d = 77 cm]
In meters it can be written as:
 $
\Rightarrow r = \dfrac{{77}}{2}cm \
\Rightarrow r = \dfrac{{77}}{{2 \times 100}}m \
  $ $ \left(
  \because 100cm = 1m \ ,
  \dfrac{{77}}{2}cm = \dfrac{1}{{100}} \times \dfrac{{77}}{2} \
  \right) $
Circumference of a circle is given as $ 2\pi r $ , substituting the values, we get:
\[
\Rightarrow 2\pi r = 2 \times \dfrac{{22}}{7} \times \dfrac{{77}}{{2 \times 100}}m \
\Rightarrow 2\pi r = \dfrac{{22 \times 11}}{{100}}m \
 \]
Let number of revolutions taken be x, then the distance covered by the bucket is \[2\pi r \times x\], substituting the values:
\[\Rightarrow 2\pi r \times x = \dfrac{{22 \times 11}}{{100}} \times xm\] __________ (1)
The total distance actually covered is given by:
\[speed = \dfrac{{dis\tan ce}}{{time}}\]
$\Rightarrow$ Distance(d) = speed X time
Speed = 1.1 m/s (given)
Time (t) = 1 minute 28 seconds
t = (60 + 28) seconds [As 1 min = 60 seconds]
t = 88 seconds
d = (1.1 X 88) m
d = \[\left( {\dfrac{{11}}{{10}} \times 88} \right){\text{ }}m\] (removing the decimal) _________ (2)
Equating (1) and (2) because both represent the distance covered by the bucket:

\[
\Rightarrow \dfrac{{22 \times 11}}{{100}} \times x = \left( {\dfrac{{11}}{{10}} \times 88} \right){\text{ }} \]

\[ x = 4 \times 10
  = 40
 \]

Therefore, the total number of complete revolutions the wheel makes in raising the bucket is 40.

Note: We do not complete the calculations in between such questions because in the end, the similar quantities cancel out. We can proceed by performing complete calculations as well but that will be a waste of time.
The number of revolutions can be calculated directly without following the long route by using the formula:
\[Number{\text{ }}of{\text{ }}revolutions{\text{ }} = {\text{ }}\dfrac{{Distance{\text{ }}covered{\text{ }}by{\text{ }}wheel}}{{circumference{\text{ }}of{\text{ }}wheel}}\]
The units are always like, initially the distance was in cm but was converted to meter because the rest of the given quantities were also in the meter.