Question

A bucket is in the form of a frustum of a cone and it can hold 28.49 liters of water. If the radii of its circular ends are 28 cm and 21 cm, find the height of the bucket. $\left[ {{\text{use }}\pi = \dfrac{{22}}{7}} \right]$

Answer 1

Hint: Here we have to go through by applying the formula of volume of frustum of cone i.e. $\dfrac{1}{3}\pi h({r_1}^2 + {r_2}^2 + {r_1}{r_2})$ where the radius of circular ends are given in the question.

Complete step-by-step answer:
Here in the question it is given that a bucket is in the form of a frustum of a cone and its can hold 28.49 liters of water and the radii of its circular ends are 28 cm and 21 cm.
For finding the height of the bucket,
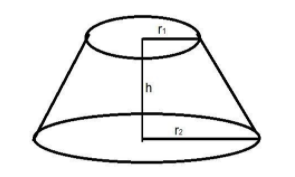
Let the height of the bucket be h cm.
Suppose ${r_1}$ and ${r_2}$ be the radii of the circular ends of the bucket.
Given, ${r_1} = 28cm$ and ${r_2} = 21cm$
And the capacity of the bucket is given as 28.49 liters
Now we have to convert this volume in the form of $c{m^3}$ for applying the formula of frustum of cone.
And as we know that 1 liter=$1000c{m^3}$.
So the volume of bucket $ = 28.49 \times 1000c{m^3}$
Now we apply the formula of frustum of cone i.e.
$
   \Rightarrow \dfrac{1}{3}\pi h({r_1}^2 + {r_2}^2 + {r_1}{r_2}) = 28.49 \times 1000 \\
   \Rightarrow \dfrac{1}{3} \times \dfrac{{22}}{7} \times h({28^2} + {21^2} + 28 \times 21) = 28490 \\
   \Rightarrow \dfrac{{22}}{{21}} \times h \times 1813 = 28490 \\
   \Rightarrow h = \dfrac{{28490 \times 21}}{{22 \times 1813}} \\
   \Rightarrow h = 15cm \\
 $
Therefore, the height of the bucket is 15 cm.

Note: Whenever we face such a type of question the key concept for solving the question is to first recall the formula of the figure that is discussed in the question and then simply put the values in that formula that are given in the question and we will automatically find out the unknown term that is being asked in the question.