Question

A bucket is 20 cm in diameter at the open end, 12 cm in diameter at the bottom, and 16 cm deep. To what depth would the bucket fill a cylindrical tin 28 cm in diameter?

Answer 1

Hint: We are given a bucket with given dimensions of upper and lower circular diameters and height and a cylindrical tin with diameter.
And we have to find the height up to which this bucket will fill the cylinder.
Extend the sides of the bucket from lower so that it forms a cone. Then, find the volume of the larger cone and volume of the smaller cone and then subtract them to get the volume of the bucket.
Then, equate this volume with the volume of the cylinder, and find the height.
Volume of cone $ = \dfrac{1}{3}\pi {r^2}h$
Volume of cylinder $ = \pi {r^2}h$

Complete step by step answer:
Given the upper diameter of the bucket $ = 20cm$ , hence the radius $ = 10cm$
Lower diameter of the bucket $ = 12cm$ , hence the radius $ = 6cm$
Height of the bucket $ = 16cm$
Diameter of the cylinder $ = 28cm$ , hence the radius $ = 14cm$
Now, Extend the sides of the bucket from lower so that it forms a cone. Then, find the volume of the larger cone and volume of the smaller cone and then subtract them to get the volume of the bucket as shown in the figure below.
Let the height of the bigger cone $ = x$

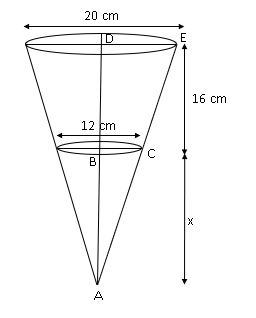
Now, consider $\Delta ABC$ and $\Delta ADC$ these two triangles are similar due to the angle-angle theorem since $\angle DAE$ is common in both triangles and $\angle ADE = \angle ABC = {90^o}$ .
Therefore, $\dfrac{{BA}}{{DA}} = \dfrac{{BC}}{{DE}}$ i.e., $\dfrac{x}{{x + 16}} = \dfrac{6}{{10}}$
On cross multiplying and solving, we get, $48 + 3x = 5x$ which gives $x = 24cm$
Thus, the height of the larger cone $ = 16 + x = 16 + 24 = 40cm$
The volume of a bigger cone $ = \dfrac{1}{3}\pi {r^2}h$ , putting values of $r$ and $h$ , we get, $\dfrac{1}{3}\pi \times 10 \times 10 \times 40 = \dfrac{{4000\pi }}{3}c{m^3}$
Now, the volume of the smaller cone $ = \dfrac{1}{3}\pi \times 6 \times 6 \times 24 = 288\pi c{m^3}$
Hence, we will get the volume of the bucket by subtracting the volume of the smaller cone from the volume of the larger cone.
So, the volume of the bucket $ = \dfrac{{4000\pi }}{3} - 288\pi = \dfrac{{3136\pi }}{3}c{m^3}$ .
Now, the volume of the cylinder filled will be equal to the volume of the bucket.
And, we know, the volume of a cylinder $ = \pi {r^2}h$
Hence, $\pi {r^2}h = \dfrac{{3136\pi }}{3}$
On putting values, we get, $\pi \times {\left( {14} \right)^2} \times h = \dfrac{{3136\pi }}{3}$ on solving gives, $h = \dfrac{{3136}}{{588}} = 5.33cm$ .

Note:Since the shape of the bucket is not something which we have studied, that is why, we have extended the sides of the bucket to form the cone, so that we can find the volume of the bucket.
Since, we have to find the height up to which the bucket will fill the cylinder, which is a matter of volume and not the surface area.
If two triangles are similar, then the corresponding sides of the triangles are proportional.