Question

A brick weighing 40N having dimensions of $25cm\times 10cm\times 5cm$ is kept on a table with its three different sides one by one. Calculate the pressure exerted in each of the three cases.

Answer 1

Hint: We are given a brick which is placed on a table. The dimensions of the brick and the weight of the brick is given. We need to change the base of the brick which exerts pressure on the table and find the pressure in different cases. Since we change the base in each case area also changes. By finding area and the force exerted by the body we can find the pressure in all cases.

Formula used:
Area $\text{A=length }\!\!\times\!\!\text{ breadth}$
Pressure, $\text{P=}\dfrac{\text{Force}}{\text{Area}}$

Complete step by step answer:
In the question we are given a block which is kept on a table and its dimensions are also given.
It is said that the weight of the body is 40 N.
The dimensions of the body is given as $25cm\times 10cm\times 5cm$
The given situation is shown in the figure below.

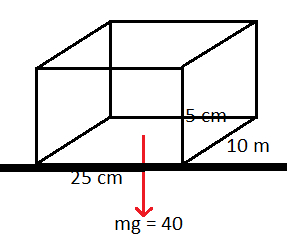
Here the only force acting on the body is the weight of the body, therefore we can say
F = 40 N
We need to find the pressure exerted by the brick on the table in all three cases.
We know that pressure is the ratio of the force exerted and the area on to which the force is exerted, i.e.
$P=\dfrac{F}{A}$, were ‘P’ is pressure, ‘F’ is the force and ‘A’ is area
We obtain the three cases when we change the base of the brick.
Therefore the first case will be with 25 cm and 10 cm as the base as shown in the figure below.

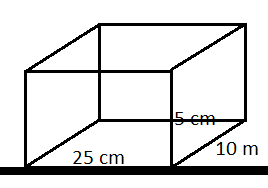
We know that the area of the base is the product of length and breadth.
Therefore area,
$\begin{align}
  & A=\left( 25\times {{10}^{-2}} \right)\times \left( 10\times {{10}^{-2}} \right) \\
 & A=250\times {{10}^{-4}} \\
\end{align}$
We know that F = 40 N.
Therefore we have pressure,
$\begin{align}
  & P=\dfrac{40}{250\times {{10}^{-4}}} \\
 & P=1.6kPa \\
\end{align}$
Now let us find the pressure in the second case.
Second case is shown in the figure below.

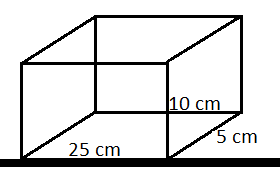
Here the base is 25 cm and 5 cm.
Therefore the area which exerts pressure,
$\begin{align}
  & A=\left( 25\times {{10}^{-2}} \right)\left( 5\times {{10}^{-2}} \right) \\
 & A=125\times {{10}^{-4}} \\
\end{align}$
Therefore the pressure exerted,
$\begin{align}
  & P=\dfrac{F}{A} \\
 & P=\dfrac{40}{125\times {{10}^{-4}}} \\
 & P=3.2\times {{10}^{3}}kPa \\
\end{align}$
The third case is shown in the figure below.

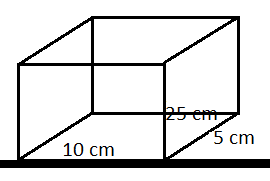
Here we take the base as 10 cm and 5 cm.
Hence the area of the base,
$\begin{align}
  & A=\left( 10\times {{10}^{-2}} \right)\left( 5\times {{10}^{-2}} \right) \\
 & A=50\times {{10}^{-4}} \\
\end{align}$
Therefore the pressure exerted,
$\begin{align}
  & P=\dfrac{40}{50\times {{10}^{-4}}} \\
 & P=8kPa \\
\end{align}$
Thus we have the pressure exerted in three cases,
First case, base as $25cm\times 10cm$, pressure $P=1.6kPa$
Second case, base as $25cm\times 5cm$, pressure $P=3.2\times {{10}^{3}}kPa$
Third case, base as $10cm\times 5cm$, pressure $P=8kPa$

Note:
Even though we change the base of the brick in each case the force exerted by the brick on the table does not change. This is because we are not changing the dimensions of the brick, i.e. the dimensions of the brick remain the same or the weight of the brick remains the same. Hence the force does not change. Since the dimensions are given in centimeters we have converted them into meters.
To convert a value in centimeter to meter we multiply it with ${{10}^{-2}}$
$1cm=1\times {{10}^{2}}m$