Question

A brick measures \[20cm \times 10cm \times 5cm\] . How many bricks would be required to build a wall of \[10m \times 15m \times 0.2m\]?

Answer 1

Hint: Cuboid is a three-dimensional shape which can be defined in a XYZ co-ordinate system having 6 faces, 8 vertices and 12 edges and the opposite faces are parallel to each other with only parallel faces are of equal dimensions

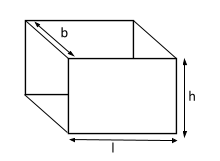
The volume of the cuboid is given by \[l \times b \times h\]

Total Surface area of cuboid is given by \[ = 2(lb + bh + lh)\]
Lateral Surface area of cuboid is given by \[ = 2(lh + bh) = 2h(l + b)\]
Lateral surface area means an area of all faces except the top and bottom face.
Where l, b and h are length, breadth and height of the cuboid respectively.
Unit of volume \[ = {m^3}\]

Complete answer: Given,
Length of the brick\[ = {l_b} = 20cm = 0.2m\]
Breadth of the brick\[ = {b_b} = 10cm = 0.1m\]
Height of the brick\[ = {h_b} = 5cm = 0.05m\]
Now, as we know that the volume of the brick \[ = {l_b} \times {b_b} \times {h_b}\]
Putting the value of lb, bb and hb in the above equation we get,
Volume of the brick\[ = (0.2 \times 0.1 \times 0.05){m^3} = 0.001{m^3}\]
Also we are given,
Length of the wall\[ = {l_w} = 10m\]
Breadth of the wall\[ = {b_w} = 0.2m\]
Height of the wall\[ = {h_w} = 15m\]

Hence, volume of the wall \[ = {l_w} \times {b_w} \times {h_w}\]
Now putting the value of lw, bw, hw we get,
Volume of the wall\[ = (10 \times 0.2 \times 15){m^3} = 30{m^3}\]
Hence we need to find that how many number of bricks of volume \[0.001{m^3}\]are required to make a wall of volume \[30{m^3}\]
That is No. of bricks will be equal to the ratio of volume of the wall to the volume of a brick,
Therefore, mathematically number of bricks \[ = \dfrac{{volume{\text{ }}of{\text{ }}the{\text{ }}wall}}{{volume{\text{ }}of{\text{ }}a{\text{ }}brick}} = \dfrac{{30}}{{0.001}} = \]30,000 bricks
Hence total no. of bricks of volume \[0.001{m^3}\] required to make a wall of volume \[30{m^3}\] is 30,000 which is the required answer

Note: Don’t confuse between the formulas. Never forget to write the correct unit in your answer. Unit of volume will always be in Cubic unit. Also the unit of length, breadth and height should be converted to a same unit. \[1m = 100cm\]