Question

A boy is standing on the ground and flying a kite with 100m of string at an elevation of 30 degree. Another boy is standing on the roof of a 10m high building and flying his kite at an elevation of 45 degree. Both the boys are on the opposite side of both the kites. Find the length of the string the second boy must have so that the two kites meet.

Answer 1

Hint: First we will draw the required diagram and then using the trigonometric formula in one triangle we will find the value of height in terms of AD and after that in another triangle we will use that value to find the length of the second string.

Complete step-by-step answer:
Let’s first draw the required diagram,

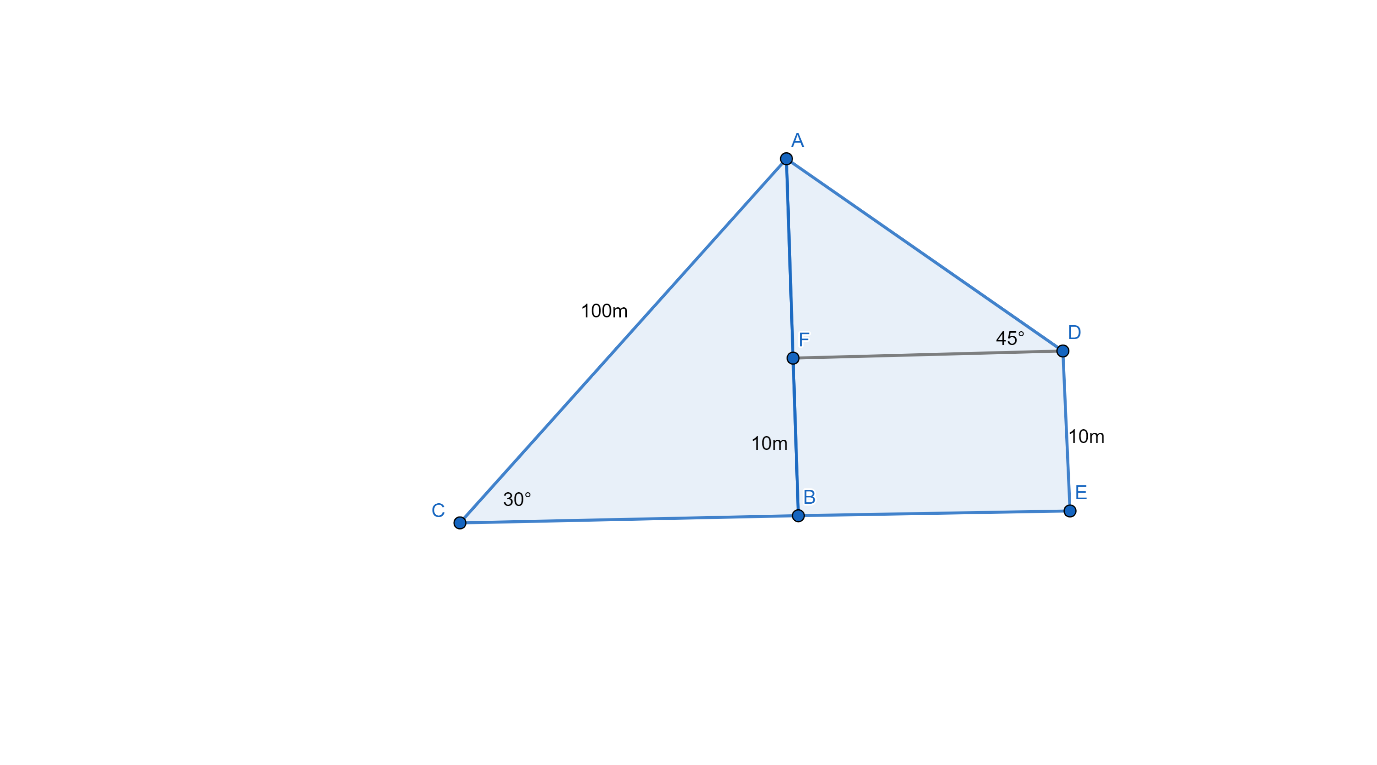
In this figure we have given,
DE= BF = 10m
AC = 100m
We need to find the value of AD.
First we will find the value of AF in terms AD
In triangle ADF, height = AF and hypotenuse = AD
Therefore,
$\sin 45=\dfrac{height}{hypotenuse}$
Substituting the value of height and hypotenuse we get,
$\begin{align}
  & \sin 45=\dfrac{AF}{AD} \\
 & AF=AD\sin 45 \\
 & AF=\dfrac{AD}{\sqrt{2}} \\
\end{align}$
From the figure we can see that,
AB = AF + BF
Using BF = 10m and AF = $\dfrac{AD}{\sqrt{2}}$ we get,
AB = $10+\dfrac{AD}{\sqrt{2}}...........(1)$
In triangle ABC, height = AB and hypotenuse = AC = 100m
$\sin 30=\dfrac{height}{hypotenuse}$
Substituting the value of height from equation (1) and hypotenuse = AC = 100 we get,
$\begin{align}
  & \sin 30=\dfrac{10+\dfrac{AD}{\sqrt{2}}}{100} \\
 & \Rightarrow \dfrac{1}{2}=\dfrac{10+\dfrac{AD}{\sqrt{2}}}{100} \\
 & \Rightarrow 50=10+\dfrac{AD}{\sqrt{2}} \\
 & \Rightarrow AD=40\sqrt{2} \\
\end{align}$
Hence the value of the second string is $40\sqrt{2}m$ .

Note: To solve such types of questions the diagram is very important, there is a good chance of making a wrong diagram and then we will get the wrong answer. So one must be careful while making the diagram. Generally students try to use the formula of tan but here we have to use sin.