Question

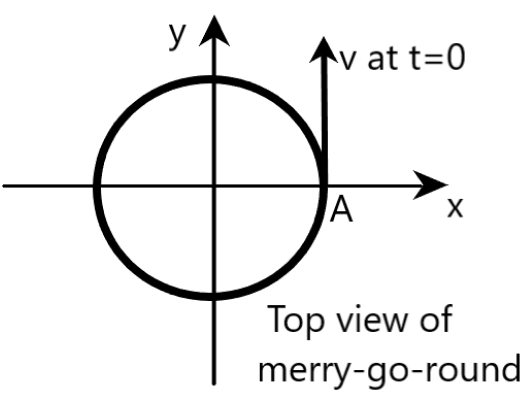
A boy is sitting on the seat of a merry-go-round with a constant angular velocity. At $t=0$, the body is at position $A$, as shown in the figure. Which of the following graphs are correct? All graphs are sinusoidal.

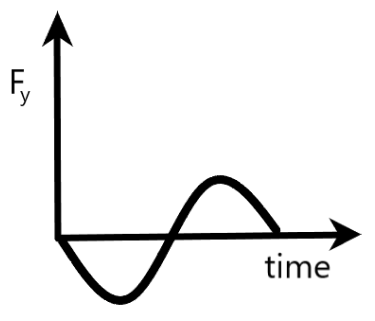
$A){{F}_{y}}$ is the $y$- component of the force keeping the boy moving in a circle

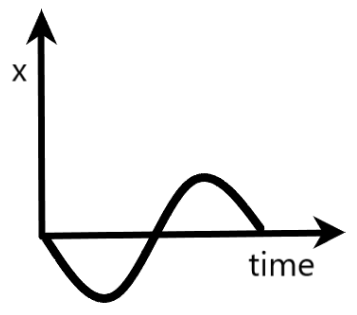
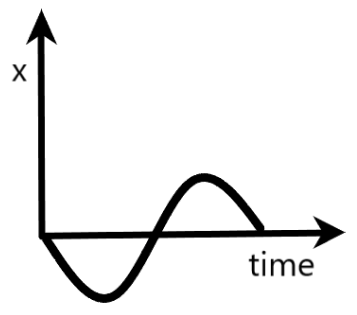
$B)x$ is the $x$-component of the boy’s position

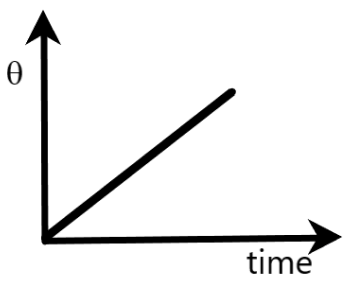
$C)\theta $ is the angle that the position vector of the boy makes with the positive $x$-axis

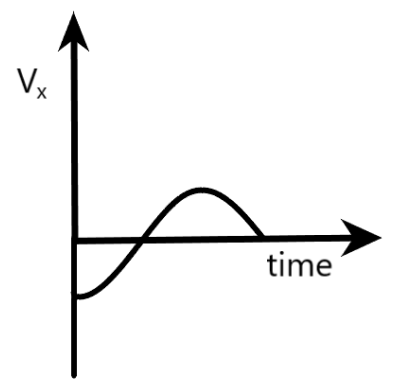
$D){{V}_{x}}$ is the $x$-component of the boy’s velocity

Answer 1

Hint: Each option is scrutinized by taking the position of the boy at a particular time $t$. When the boy moves from his initial position at $t=0$ to a position at time $t$, the angular displacement of the boy is taken as $\theta $. Then, the required equations are derived and checked with the given graphs, one by one.

Complete step-by-step solution
We are given that a boy is sitting on the seat of a merry-go-round with a constant angular velocity. At $t=0$, the body is at position $A$. We are also provided with four graphs, which talks about different parameters with respect to the movement of boys in the merry-go-round. We are required to mark the correct graphs from these options.
For this, let us assume that the boy has already started moving in the merry-go-round and is at a position $B$ now, as shown in the figures given below. Let $t$ be the time at which the boy is at $B$, as shown.
Now, let us go through the provided options one by one.
$A){{F}_{y}}$ is the $y$- component of the force keeping the boy moving in a circle

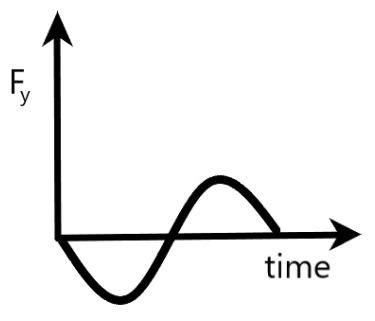
Here, we are told that ${{F}_{y}}$ is the $y$- component of the force keeping the boy moving in a circle. From the graph, it is clear that ${{F}_{y}}$ is in the form of a negative sinusoidal wave, moving with respect to time.
Now, let’s have a look at the figure given below.

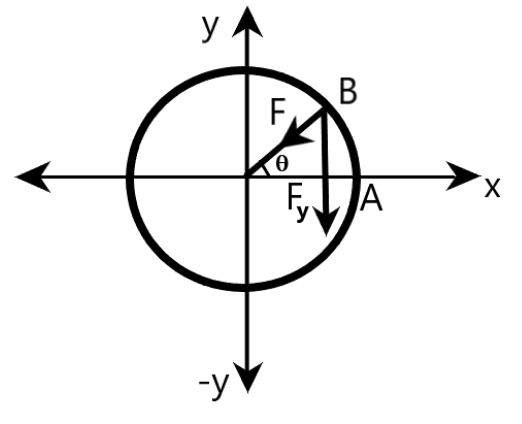
Clearly, the boy is at $B$, when the time is $t$. We know that force acting on the boy is the centripetal force, which is given by
$F=m{{\omega }^{2}}r$
where
$F$ is the centripetal force acting on the boy at time $t$
$m$ is the mass of the boy
$\omega $ is the angular frequency of motion of the boy
$r$ is the radius of the merry-go-round
Clearly, the centripetal force is acting along the position vector of the boy at $B$, as shown.
Now, the $y$-component of this centripetal force is given by
${{F}_{y}}=-m{{\omega }^{2}}r\sin \theta =-m{{\omega }^{2}}r\sin (\omega t)$
where
${{F}_{y}}$ is the $y$-component of the centripetal force
$\theta =\omega t$ is the angular displacement of the boy
Clearly, this component of force is acting along the negative $y$-direction
Also, if we draw a graph between ${{F}_{y}}$ and $t$, it is of the form of a negative sine wave.
The graph given in option $A$ satisfies this condition and hence, we can conclude that option $A$ is correct.
$B)x$ is the $x$-component of the boy’s position

$x$-component of the position vector of the boy at $B$ can be deduced from the right triangle $CEB$, as shown below.

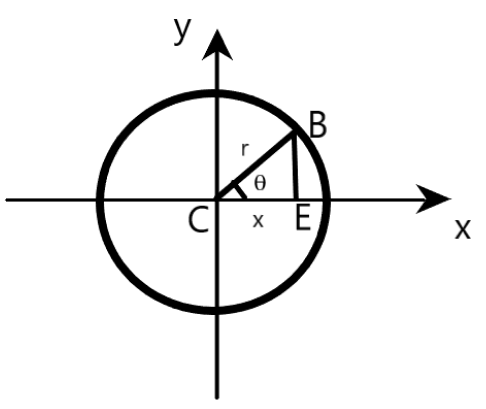
Clearly, $x$-component of the position vector of the boy at $B$ is given by
$x=r\cos \theta =r\cos (\omega t)$
where
$x$ is the $x$-component of the position vector of the boy at $B$
$r$ is the radius of the merry-go-round
$\theta =\omega t$ is the angular displacement of the motion of the boy
Now, if we draw a graph between $x$ and $t$, it will have the shape of a cosine wave. Since the graph provided in the option is in the form of a sine wave, the given option is concluded as wrong.
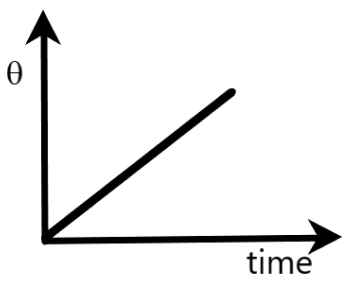
$C)\theta $ is the angle that the position vector of the boy makes with the positive $x$-axis

We know that angular frequency is defined as angular displacement per unit time. If $\omega $ represents the angular frequency of the boy rotating in merry-go-round at time $t$, then, $\omega $ is given by
$\omega =\dfrac{\theta }{t}\Rightarrow \theta =\omega t$
where
$\omega $ is the angular frequency of the boy at time $t$
$\theta $ is the angular displacement of the boy at time $t$
Clearly, angular displacement is directly proportional to time. Therefore, if we draw a graph between $\theta $ and $t$, it will look similar to the graph provided in the option, as given above.
Hence, option $C$ is also correct.
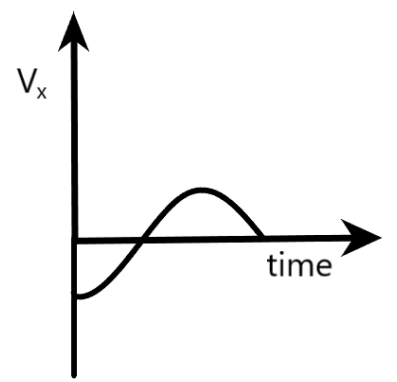
$D){{V}_{x}}$ is the $x$-component of the boy’s velocity

Here, we are said that ${{V}_{x}}$ is the $x$-component of the boy’s velocity $x$-component of the velocity vector of the boy at $B$ can be deduced from the right triangle $CFB$, where $< B = \theta $, as shown below.

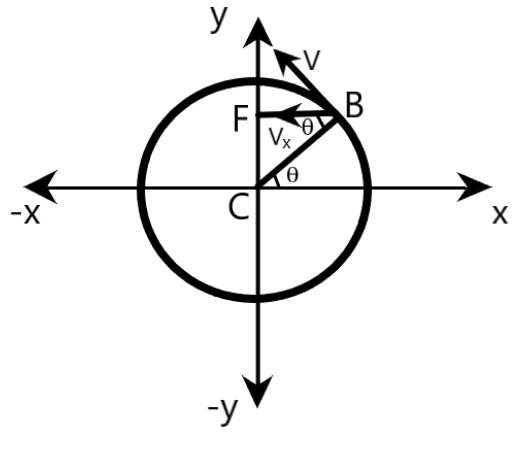
Here, the velocity of the boy at $B$ is given by
$V=\omega r$
where
$V$ is the velocity of the boy at $B$
$\omega $ is the angular frequency of the motion of boy at time $t$
$r$ is the radius of the merry-go-round
Clearly, this velocity is acting along the tangent drawn at $B$, as shown in the figure.
Now, the $x$-component of this velocity is given by
${{V}_{x}}=-\omega r\sin \theta =-\omega r\sin (\omega t)$
where
${{V}_{x}}$ is the $x$-component velocity of the boy at $B$
$\theta =\omega t$ is the angular displacement of the boy at $t$
Clearly, this component of velocity acts in the negative $x$-direction. If we draw a graph between ${{V}_{x}}$
and $t$, it will have the shape of a negative sine wave.
Since the provided option has the shape of a negative cosine wave, option $D$ can be concluded as wrong.
Therefore, option $A$ and option $C$ is correct while option $B$ and option $D$ are incorrect for a boy moving in a merry-go-round.

Note: Such questions are asked to evaluate the visualizing capabilities of students. Therefore, students need to be thorough with the shapes of a positive sine wave, a negative sine wave, a positive cosine wave, and a negative cosine wave. Deducing the correct waveform from an equation is also important, which students should practice from time to time.