Question

A boy is hanging from a horizontal branch of a tree. The tension in the arms will be maximum when the angle between the arms is
A. $0^\circ$
B. $30^\circ$
C. $60^\circ$
D. $120^\circ$

Answer 1

Hint:There are only 2 forces acting on the boy: Weight and Tension. The tension will be produced in his arms as a reaction to the weight of the boy which is pointed vertically, downwards. Hence, by drawing a free-body diagram, we can understand the relationship between the tension and the weight of the boy.

Complete step-by-step answer:
Let the angle between each of the arm and the vertical axis be equal to $\theta $
Now, we have to draw the free-body diagram of the boy hanging from the branch of a tree.
The free-body diagram is a diagram where the entire mass of the system is represented by a block of mass m and all the forces acting on it are displayed.
So, let us draw the free-body diagram of the above case:

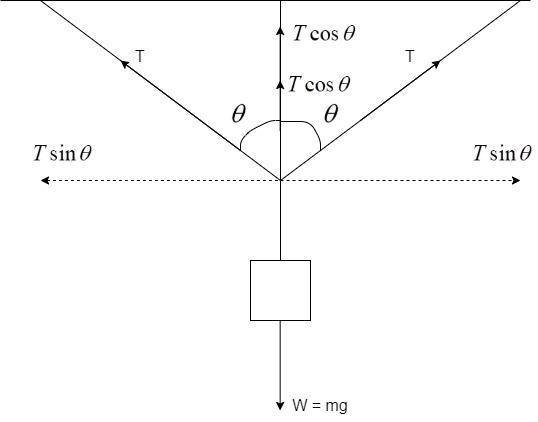
So, in the above free-body diagram, we can see that there are two major forces acting on the boy: i) Weight of the boy, W = mg where m is the mass of the boy and g is the acceleration due to gravity. ii) Tension in the arms, T.
Now, the tension T can be split into two components: horizontal $T\sin \theta $ and vertical $T\cos \theta $ as shown in the free-body diagram.
By equating the forces along the X and Y axis, we get –
X: $T\sin \theta = T\sin \theta $
Since equal forces are acting, they cancel out each other and hence, there is no net force acting in the X-direction.
Y: $W = T\cos \theta + T\cos \theta $
Adding them, we get –
$W = 2T\cos \theta $
Solving,
$T = \dfrac{W}{{2\cos \theta }}$
Here, we see that the value of tension is proportional to $\cos \theta $.
This means that the value of the tension will be highest when the value of $\cos \theta = 1$
Thus, $\theta = {\cos ^{ - 1}}\left( 1 \right) = {0^ \circ }$
Thus, $2\theta = {0^ \circ }$
So, when the angle between the arms is \[{0^ \circ }\], we see that the tension on the arms is maximum and the tension decreases as the arms go wider apart from each other.

Hence, the correct option is Option A.

Note: Whenever you are performing the exercise known as pull-up in the gym, notice that the maximum pull on the muscle happens when the arms are closer to each, because of the reason explained in the solution. Thus, the maximum amount of the body weight will be applied as tension on the biceps and triceps muscles in the arm. The more the tension applied on the muscles in arms, the better is the workout.