Question

A boy is flying a kite with a string of length $100m$. If the string is tight and the angle of elevation of the kite is \[26^\circ 32'\], find the height of the kite corrects to two decimal places (ignore the height of the boy).
A) $44.67m$
B) $53.87m$
C) $34.78m$
D) $42.87m$

Answer 1

Hint:This is the question of height and distance. First, we draw the figure of the question in order to understand the angle and distance of the kite and then apply trigonometric ratios to evaluate the height of the kite.

Complete step-by-step answer:
We are given that a boy is flying a kite with a string of length $100m$. If the string is tight and the angle of elevation of the kite is \[26^\circ 32'\].
We draw the figure according to the given conditions.

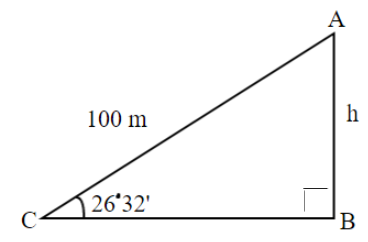
Let the height AB of the kite is $h$
We have to evaluate the height of the kite.
The length of string is denoted by AC which is $100m$.
Now we are able to see that AB denotes the altitude of the triangle and AC denotes the hypotenuse of the triangle.
Use the trigonometric ratio which involves the ratio of the altitude to the hypotenuse.
We know that,
$\sin \theta = \dfrac{{Altitude}}{{Hypotenuse}}......(1)$
Here $\theta $ is the base angle.
In our question $\theta = 26^\circ 32'$
Substitute the values in the equation $(1)$
$
  \sin (26^\circ 32') = \dfrac{{AB}}{{AC}} \\
  \sin (26^\circ 32') = \dfrac{h}{{100}} \\
  h = 100\sin (26^\circ 32') \\
 $
Substitute $\sin (26^\circ 32') = 0.44671$
$
  h = 100 \times 0.44671 \\
  h = 44.67m \\
 $
Therefore, the height of the kite is $44.67m$.

Note:
We can solve this question by using another trigonometric ratio which is shown below:
We know that the cosecant function is the ratio of the hypotenuse to the altitude.
Therefore,
\[
  \cos ec(26^\circ 32') = \dfrac{{100}}{h} \\
  h = \dfrac{{100}}{{\cos ec(26^\circ 32')}} \\
 \]
Substitute $\cos ec(26^\circ 32') = 2.2385$
$
  h = \dfrac{{100}}{{2.2385}} \\
  h = 44.67m \\
 $
Therefore, the height of the kite is $44.67m$.
Hence, option (A) is correct.