Question

A boy 2m long casts a shadow 1m long on the plane ground. At the same time, a tower casts a shadow 5m long on the ground. Find the height of the tower(in m).

Answer 1

Hint: Take AB=2m as the height of the boy and assume the height of tower PQ be x. Find the angle of elevation in the \[\Delta ABC\] using tan formula. Now, in \[\Delta DEF\], the angle of elevation is the same as in earlier cases. Use tan of angle of elevation and then find the value of x after solving it.

Complete step-by-step answer:
According to the question for case 1st , it is given that
Height of boy = 2 m.
Length of shadow formed on the ground = 1 m.
Take AB as the height of the boy and BC as the length of the shadow.

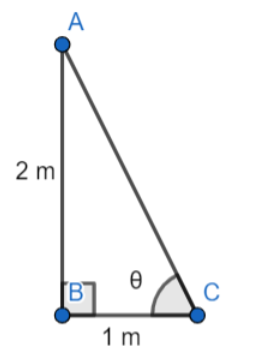
Let us assume the angle of elevation as,
\[\angle ACB=\theta \] ……………………(1)
In the \[\Delta ABC\] , we have
AB = 2 m.
BC = 1 m.
\[\tan \theta =\dfrac{AB}{BC}\]
\[\Rightarrow \tan \theta =\dfrac{2}{1}\] …………………(2)
In case 2nd, we have a tower which casts a shadow of 5m on the ground.
Let the height of the tower be x.
Length of shadow formed on the ground = 5 m.
Take DE as the height of the tower and EF as the length of the shadow.

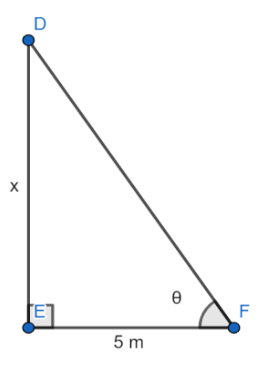
Angle of elevation will be the same as in case 1st .
\[\angle DFE=\angle ACB=\theta \]
In the \[\Delta DEF\] , we have
DE = x m.
EF = 5 m.
\[\tan \theta =\dfrac{DE}{EF}\]
Using equation (2) and putting the value of EF = 5m we get,
\[\begin{align}
  & 2=\dfrac{x}{5} \\
 & \Rightarrow x=10 \\
\end{align}\]
Hence, the height of the tower is 10m.

Note: In this question, one may get confused because we have taken the angle of elevation equal in both cases. As the tower is also forming shadow at the same time when the boy is casting a shadow of 1m. So, the angle of light at which the light falls on the boy and tower will be the same due to which our angle of elevation will be the same.