Question

A box of mass m is attached to a spring on a frictionless surface. The spring is compressed from its equilibrium position, B, to point A, a distance x from B. Point C is also a distance x from B, but in the opposite direction. When the box is released from position A? Find out the points at which box's velocity is maximum?
 

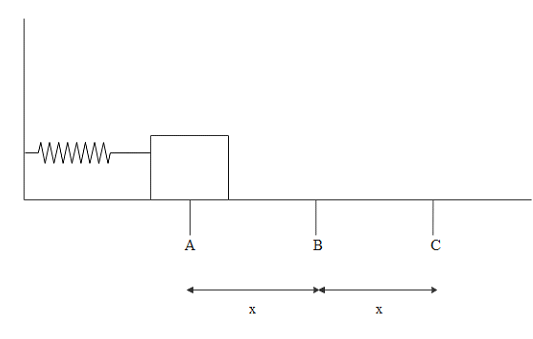
A. A
B. B
C. C
D. Both A and C

Answer 1

Hint: When some amount of work is done against the conservative force then the work done will be stored in the system as the potential energy as energy can neither be created nor destroyed. Along the direction of conservative force then potential energy of the system decreases. By using these two principles we will solve the question.

Complete step by step answer:
In spring, as long as spring is in natural length it doesn’t have any energy. If we apply force to elongate it or compress it then the elongation or compression is produced in it and potential energy will be stored in the spring.
The spring force which opposes the applied force will be $F = - Kx$

Where ‘K’ is the force constant and ‘x’ is the elongation or compression produced and the negative sign indicates that spring force opposes the direction of change.
Initially for the spring at position B there is no energy. The amount of work done to increase or decrease its length will be stored as internal potential energy.
Initial energy = 0
Work done to create the compression ‘x’ is $W = F.x = (Kx)(x) = K{x^2}$
So this is converted to the energy and hence the final energy = $K{x^2}$
Now as the spring force varies linearly with elongation, force is not constant and it varies at every instant and it is the same in case of work done so work also varies which means energy at every instant also varies.
Even though energy at every instant is varying we know the initial energy and the final energy we take the average of to find out the energy stored.
In this spring case at compression $x$ at point A the final energy is $K{x^2}$
So average energy is $\dfrac{{0 + K{x^2}}}{2} = \dfrac{1}{2}K{x^2}$
So the overall potential energy stored at A and C is $\dfrac{1}{2}K{x^2}$
Since the mass is only acted upon the spring force and gravitational force, both are conservative forces and the work is done only by the spring force as gravitational force is perpendicular to the displacement of the mass, according to conservation of mechanical energy, total mechanical energy of the system is always conserved as long as only conservative forces acting on it.
That means change in mechanical energy is zero and mechanical energy(ME) will be constant always. Mechanical energy is the sum of potential and kinetic energy
$ ME = {\text{ constant}} $
$ KE + PE = {\text{constant}} $
$ \dfrac{1}{2}k{x^2} + \dfrac{1}{2}m{v^2} = {\text{constant}} $
Where ‘x’ is the elongation or compression of spring and ‘k’ is the force constant of the spring and ‘m’ is the mass of the block and ‘v’ is the velocity of the block.
So from the above expression, if potential energy is maximum then kinetic energy should be minimum and if potential energy is minimum then kinetic energy should be maximum as the total sum is constant.
From the given question at position B potential energy will be minimum as at that position spring is at natural length, there will be no elongation or compression. So at position B kinetic energy is maximum and hence velocity is maximum at B as kinetic energy is proportional to the velocity.

So option B will be the answer.

Note:
The energy stored in the spring is only half the work done. One might doubt where the other half of work has gone. The other half of the work is lost as heat. We can also consider this case as S.H.M with B as the mean position and A, C are extreme positions. Hence velocity will be maximum at mean position in case of S.H.M.