Question

A body starts from rest and travels a distance S with uniform acceleration, then moves uniformly a distance 2S and finally comes to rest after moving further 5S under uniform retardation. The ratio of the average velocity to maximum velocity is
(a) 2/5
(b) 3/5
(c) 4/7
(d) 5/7

Answer 1

Hint: Use the concept of Motion In A Straight Line. Area of triangle= $\dfrac{1}{2}\times{base}\times{height}$ and Area of rectangle = ${base}\times{height}$.

Complete step by step solution:
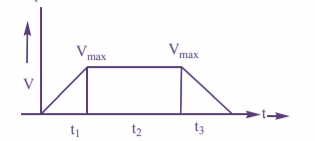
Area of the (V–t) curve represents displacement.

$
  S = \dfrac{1}{2}{v_{\max }}{t_1} \Rightarrow {t_1} = \dfrac{{2S}}{{{v_{\max }}}} \\
  2S = \dfrac{1}{2}{v_{\max }}{t_2} \Rightarrow {t_2} = \dfrac{{2S}}{{{v_{\max }}}} \\
  5S = \dfrac{1}{2}{v_{\max }}{t_2} \Rightarrow {t_3} = \dfrac{{10S}}{{{v_{\max }}}} \\
$
${V_{avg}} = \dfrac{{{\text{Total displacement}}}}{{{\text{Total time}}}}$$\dfrac{{S + 2S + 5S}}{{\dfrac{{2S}}{{{v_{\max }}}} + \dfrac{{2S}}{{{v_{\max }}}} + \dfrac{{10S}}{{{v_{\max }}}}}} = \dfrac{{8S}}{{\left( {\dfrac{{14S}}{{{v_{\max }}}}} \right)}} = {v_{\max }}\dfrac{4}{7}$
The ratio of the average velocity to maximum velocity= \[\dfrac{{{v_{avg}}}}{{{v_{\max }}}} = \dfrac{{{v_{\max }}\dfrac{4}{7}}}{{{v_{\max }}}} = \dfrac{4}{7}\]

Correct Answer: (c) 4/7

Note: Alternative Method-
\[\dfrac{{{v_{avg}}}}{{{v_{\max }}}} = \dfrac{{Total{\text{ }}displacement}}{{2({\text{Total displacement during acceleration and retardation) + (Displacement During uniform velocity)}}}}\]
$\therefore \dfrac{{{v_{avg}}}}{{{v_{\max }}}} = \dfrac{{8S}}{{2(S + 5S) + 2S}} = \dfrac{8}{{14}} = \dfrac{4}{7}$